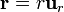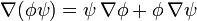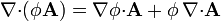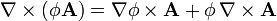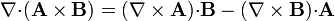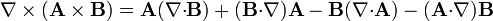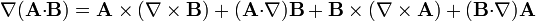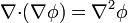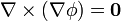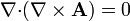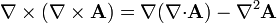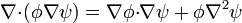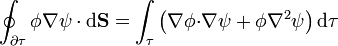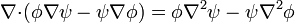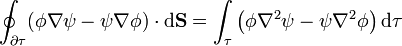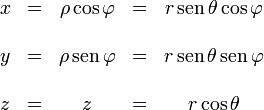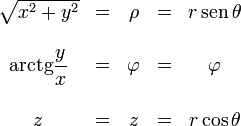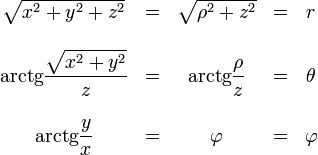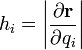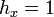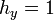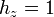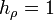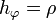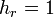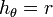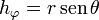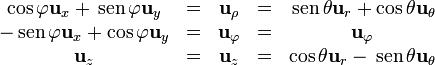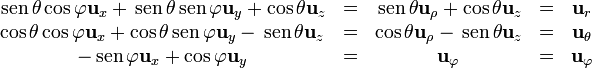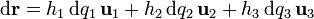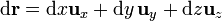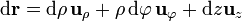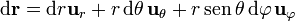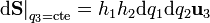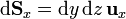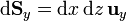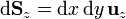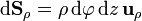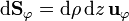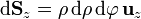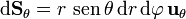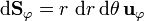Tabla de cálculo vectorial
De Laplace
(Diferencias entre revisiones)
(→=De dos campos escalares) |
(→En esféricas) |
||
| (58 ediciones intermedias no se muestran.) | |||
| Línea 7: | Línea 7: | ||
:<math>\nabla\times(\phi\mathbf{A}) = \nabla\phi\times\mathbf{A}+\phi\,\nabla\times\mathbf{A}</math> | :<math>\nabla\times(\phi\mathbf{A}) = \nabla\phi\times\mathbf{A}+\phi\,\nabla\times\mathbf{A}</math> | ||
====De dos campos vectoriales==== | ====De dos campos vectoriales==== | ||
| - | :<math>\nabla{\cdot}(\mathbf{A}\times\mathbf{B}) | + | :<math>\nabla{\cdot}(\mathbf{A}\times\mathbf{B}) = |
(\nabla\times\mathbf{A}){\cdot}\mathbf{B}-(\nabla\times\mathbf{B}){\cdot}\mathbf{A}</math> | (\nabla\times\mathbf{A}){\cdot}\mathbf{B}-(\nabla\times\mathbf{B}){\cdot}\mathbf{A}</math> | ||
| - | :<math>\nabla\times(\mathbf{A}\times\mathbf{B}) | + | :<math>\nabla\times(\mathbf{A}\times\mathbf{B}) = \mathbf{A}(\nabla{\cdot}\mathbf{B})+ |
(\mathbf{B}{\cdot}\nabla)\mathbf{A}-\mathbf{B}(\nabla{\cdot}\mathbf{A})-(\mathbf{A}{\cdot}\nabla)\mathbf{B}</math> | (\mathbf{B}{\cdot}\nabla)\mathbf{A}-\mathbf{B}(\nabla{\cdot}\mathbf{A})-(\mathbf{A}{\cdot}\nabla)\mathbf{B}</math> | ||
| - | :<math>\nabla(\mathbf{A}{\cdot}\mathbf{B}) | + | :<math>\nabla(\mathbf{A}{\cdot}\mathbf{B}) = \mathbf{A}\times(\nabla\times\mathbf{B})+(\mathbf{A}{\cdot}\nabla)\mathbf{B}+\mathbf{B}\times(\nabla\times\mathbf{A})+(\mathbf{B}{\cdot}\nabla)\mathbf{A}</math> |
| + | |||
| + | ===Operadores de segundo orden=== | ||
| + | :<math>\nabla{\cdot}(\nabla\phi) = \nabla^2\phi</math> | ||
| + | :<math>\nabla\times(\nabla\phi) = \mathbf{0}</math> | ||
| + | :<math>\nabla{\cdot}(\nabla\times\mathbf{A}) = 0</math> | ||
| + | :<math>\nabla\times(\nabla\times\mathbf{A}) = \nabla(\nabla{\cdot}\mathbf{A})-\nabla^2\mathbf{A}</math> | ||
| + | |||
| + | ===Identidades de Green=== | ||
| + | ====Primera==== | ||
| + | =====En forma diferencial===== | ||
| + | :<math>\nabla{\cdot}(\phi\nabla\psi)=\nabla\phi{\cdot}\nabla\psi+\phi\nabla^2\psi</math> | ||
| + | =====En forma integral===== | ||
| + | :<math>\oint_{\partial\tau}\phi\nabla\psi\cdot\mathrm{d}\mathbf{S}=\int_\tau\left(\nabla\phi{\cdot}\nabla\psi+\phi\nabla^2\psi\right)\mathrm{d}\tau</math> | ||
| + | |||
| + | ====Segunda==== | ||
| + | =====En forma diferencial===== | ||
| + | :<math>\nabla{\cdot}(\phi\nabla\psi-\psi\nabla\phi)=\phi\nabla^2\psi-\psi\nabla^2\phi</math> | ||
| + | |||
| + | =====En forma integral===== | ||
| + | :<math>\oint_{\partial\tau}(\phi\nabla\psi-\psi\nabla\phi)\cdot\mathrm{d}\mathbf{S}=\int_\tau\left(\phi\nabla^2\psi-\psi\nabla^2\phi\right)\mathrm{d}\tau</math> | ||
| + | |||
| + | ==Relación entre los sistemas de coordenadas== | ||
| + | ===De cartesianas a otros sistemas=== | ||
| + | |||
| + | :<math>\begin{array}{ccccc} | ||
| + | x & = & \rho\cos\varphi & =& r\,\operatorname{sen}\,\theta\cos\varphi \\&&&&\\ | ||
| + | y &=&\rho\,\operatorname{sen}\,\varphi & = & r\,\operatorname{sen}\,\theta\,\operatorname{sen}\,\varphi\\&&&&\\ | ||
| + | z &=& z &=& r\cos\theta\end{array}</math> | ||
| + | |||
| + | ===De cilíndricas a otros sistemas=== | ||
| + | |||
| + | :<math>\begin{array}{ccccc}\sqrt{x^2+y^2} &=& \rho &=& r\,\operatorname{sen}\,\theta \\ &&&& \\ | ||
| + | \operatorname{arctg}\displaystyle\frac{y}{x} &=& \varphi &=& \varphi \\&&&&\\ | ||
| + | z &=& z&=& r\cos\theta\end{array}</math> | ||
| + | |||
| + | ===De esféricas a otros sistemas=== | ||
| + | |||
| + | :<math>\begin{array}{ccccc}\sqrt{x^2+y^2+z^2}&= & \sqrt{\rho^2+z^2}&=& r \\&&&&\\ | ||
| + | \operatorname{arctg}\displaystyle\frac{\sqrt{x^2+y^2}}{z} & = & | ||
| + | \operatorname{arctg}\displaystyle\frac{\rho}{z}&=& \theta \\&&&&\\ | ||
| + | \operatorname{arctg}\displaystyle\frac{y}{x}& =& \varphi &=& \varphi\end{array}</math> | ||
| + | |||
| + | ==Vector de posición== | ||
| + | ===En cartesianas=== | ||
| + | <math>\mathbf{r}=x\mathbf{u}_{x}+y\,\mathbf{u}_{y}+z\mathbf{u}_{z}</math> | ||
| + | ===En cilíndricas=== | ||
| + | <math>\mathbf{r}=\rho\,\mathbf{u}_{\rho}+z\mathbf{u}_{z}</math> | ||
| + | ===En esféricas=== | ||
| + | <math>\mathbf{r}=r\mathbf{u}_{r}</math> | ||
| + | |||
| + | ==[[Bases vectoriales|Factores de escala]]== | ||
| + | ===Definición=== | ||
| + | :<math>h_i=\left|\frac{\partial \mathbf{r}}{\partial q_i}\right|</math> | ||
| + | |||
| + | ===Cartesianas=== | ||
| + | :<math>h_x=1\,</math>{{qquad}}<math>h_y=1\,</math>{{qquad}}<math>h_z=1\,</math> | ||
| + | |||
| + | ===Cilíndricas=== | ||
| + | :<math>h_\rho=1\,</math>{{qquad}}<math>h_\varphi=\rho</math>{{qquad}}<math>h_z=1\,</math> | ||
| + | |||
| + | ===Esféricas=== | ||
| + | :<math>h_r=1\,</math>{{qquad}}<math>h_\theta=r\,</math>{{qquad}}<math>h_\varphi=r\,\operatorname{sen}\,\theta</math> | ||
| + | |||
| + | ==Relación entre bases vectoriales== | ||
| + | ===De cartesianas a otro sistema=== | ||
| + | :<math>\begin{array}{ccccc} | ||
| + | \mathbf{u}_{x} & = & \cos\varphi\mathbf{u}_{\rho}-\,\operatorname{sen}\,\varphi\mathbf{u}_{\varphi} & = & | ||
| + | \,\operatorname{sen}\,\theta\cos\varphi\mathbf{u}_{r}+\cos\theta\cos\varphi\mathbf{u}_{\theta}-\,\operatorname{sen}\,\varphi\mathbf{u}_{\varphi} \\ | ||
| + | \mathbf{u}_{y} & = & \,\operatorname{sen}\,\varphi\mathbf{u}_{\rho}+\cos\varphi\mathbf{u}_{\varphi} & = & | ||
| + | \,\operatorname{sen}\,\theta\,\operatorname{sen}\,\varphi\mathbf{u}_{r}+\cos\theta\,\operatorname{sen}\,\varphi\mathbf{u}_{\theta}+\cos\varphi\mathbf{u}_{\varphi} \\ | ||
| + | \mathbf{u}_{z} & = & \mathbf{u}_{z} & = & \cos\theta\mathbf{u}_{r}-\,\operatorname{sen}\,\theta\mathbf{u}_{\theta} | ||
| + | \end{array}</math> | ||
| + | |||
| + | ===De cilíndricas a otro sistema=== | ||
| + | :<math>\begin{array}{ccccc} | ||
| + | \cos\varphi\mathbf{u}_{x}+\,\operatorname{sen}\,\varphi\mathbf{u}_{y} & = & \mathbf{u}_{\rho} & = & | ||
| + | \,\operatorname{sen}\,\theta\mathbf{u}_{r}+\cos\theta\mathbf{u}_{\theta} \\ | ||
| + | -\,\operatorname{sen}\,\varphi\mathbf{u}_{x}+\cos\varphi\mathbf{u}_{y} | ||
| + | & = & | ||
| + | \mathbf{u}_{\varphi}& = & | ||
| + | \mathbf{u}_{\varphi} \\ | ||
| + | \mathbf{u}_{z} & = & \mathbf{u}_{z} & = & \cos\theta\mathbf{u}_{r}-\,\operatorname{sen}\,\theta\mathbf{u}_{\theta}\\ | ||
| + | \end{array}</math> | ||
| + | |||
| + | ===De esféricas a otro sistema=== | ||
| + | :<math>\begin{array}{ccccc} | ||
| + | \,\operatorname{sen}\,\theta\cos\varphi\mathbf{u}_{x}+\,\operatorname{sen}\,\theta\,\operatorname{sen}\,\varphi\mathbf{u}_{y}+\cos\theta\mathbf{u}_{z} & = & \,\operatorname{sen}\,\theta\mathbf{u}_{\rho}+\cos\theta\mathbf{u}_{z} & = & | ||
| + | \mathbf{u}_{r} \\ | ||
| + | \cos\theta\cos\varphi\mathbf{u}_{x}+\cos\theta\,\operatorname{sen}\,\varphi\mathbf{u}_{y}-\,\operatorname{sen}\,\theta\mathbf{u}_{z} & = &\cos\theta\mathbf{u}_{\rho}-\,\operatorname{sen}\,\theta\mathbf{u}_{z} & = & | ||
| + | \mathbf{u}_{\theta} \\ | ||
| + | -\,\operatorname{sen}\,\varphi\mathbf{u}_{x}+\cos\varphi\mathbf{u}_{y} | ||
| + | & = & | ||
| + | \mathbf{u}_{\varphi}& = & | ||
| + | \mathbf{u}_{\varphi} \\ | ||
| + | \end{array}</math> | ||
| + | |||
| + | ==Diferenciales== | ||
| + | ===De camino=== | ||
| + | ====Para coordenadas ortogonales==== | ||
| + | :<math>\mathrm{d}\mathbf{r}=h_1\,\mathrm{d}q_1\,\mathbf{u}_{1}+h_2\,\mathrm{d}q_2\,\mathbf{u}_{2}+h_3\,\mathrm{d}q_3\,\mathbf{u}_{3}</math> | ||
| + | |||
| + | ====En cartesianas==== | ||
| + | :<math>\mathrm{d}\mathbf{r}=\mathrm{d}x\mathbf{u}_{x}+\mathrm{d}y\,\mathbf{u}_{y}+\mathrm{d}z\mathbf{u}_{z}</math> | ||
| + | ====En cilíndricas==== | ||
| + | :<math>\mathrm{d}\mathbf{r}=\mathrm{d}\rho\,\mathbf{u}_{\rho}+\rho\,\mathrm{d}\varphi\,\mathbf{u}_{\varphi}+\mathrm{d}z\mathbf{u}_{z}</math> | ||
| + | ====En esféricas==== | ||
| + | :<math>\mathrm{d}\mathbf{r}=\mathrm{d}r\mathbf{u}_{r}+r\,\mathrm{d}\theta\,\mathbf{u}_{\theta}+r\,\operatorname{sen}\,\theta\,\mathrm{d}\varphi\,\mathbf{u}_{\varphi}</math> | ||
| + | |||
| + | ===De superficie=== | ||
| + | ====Para coordenadas ortogonales==== | ||
| + | :<math>\left.\mathrm{d}\mathbf{S}\right|_{q_3=\mathrm{cte}}= h_1 h_2 \mathrm{d}q_1 \mathrm{d}q_2 \mathbf{u}_{3}</math> | ||
| + | ====En cartesianas==== | ||
| + | :<math>\mathrm{d}\mathbf{S}_x=\mathrm{d}y\,\mathrm{d}z\,\mathbf{u}_{x}</math> | ||
| + | :<math>\mathrm{d}\mathbf{S}_y=\mathrm{d}x\,\mathrm{d}z\,\mathbf{u}_{y}</math> | ||
| + | :<math>\mathrm{d}\mathbf{S}_z=\mathrm{d}x\,\mathrm{d}y\,\mathbf{u}_{z}</math> | ||
| + | |||
| + | ====En cilíndricas==== | ||
| + | :<math>\mathrm{d}\mathbf{S}_\rho=\rho\,\mathrm{d}\varphi\,\mathrm{d}z\,\mathbf{u}_{\rho}</math> | ||
| + | :<math>\mathrm{d}\mathbf{S}_\varphi=\mathrm{d}\rho\,\mathrm{d}z\,\mathbf{u}_{\varphi}</math> | ||
| + | :<math>\mathrm{d}\mathbf{S}_z=\rho\,\mathrm{d}\rho\,\mathrm{d}\varphi\,\mathbf{u}_{z}</math> | ||
| + | |||
| + | ====En esféricas==== | ||
| + | :<math>\mathrm{d}\mathbf{S}_r=r^2\,\,\operatorname{sen}\,\theta\,\mathrm{d}\theta\,\mathrm{d}\varphi\,\mathbf{u}_{r}</math> | ||
| + | :<math>\mathrm{d}\mathbf{S}_\theta=r\,\,\operatorname{sen}\,\theta\,\mathrm{d}r\,\mathrm{d}\varphi\,\mathbf{u}_{\theta}</math> | ||
| + | :<math>\mathrm{d}\mathbf{S}_\varphi=r\,\,\mathrm{d}r\,\mathrm{d}\theta\,\mathbf{u}_{\varphi}</math> | ||
| + | |||
| + | ===De volumen=== | ||
| + | ====Para coordenadas ortogonales==== | ||
| + | ====En cartesianas==== | ||
| + | ====En cilíndricas==== | ||
| + | ====En esféricas==== | ||
última version al 10:52 25 jul 2008
Contenido
|
1 Álgebra del operador nabla
1.1 Aplicación sobre productos
1.1.1 De dos campos escalares
1.1.2 De un campo escalar por uno vectorial
1.1.3 De dos campos vectoriales
1.2 Operadores de segundo orden
1.3 Identidades de Green
1.3.1 Primera
1.3.1.1 En forma diferencial
1.3.1.2 En forma integral
1.3.2 Segunda
1.3.2.1 En forma diferencial
1.3.2.2 En forma integral
2 Relación entre los sistemas de coordenadas
2.1 De cartesianas a otros sistemas
2.2 De cilíndricas a otros sistemas
2.3 De esféricas a otros sistemas
3 Vector de posición
3.1 En cartesianas
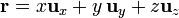
3.2 En cilíndricas
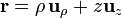
3.3 En esféricas