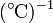Dilatación y compresibilidad (GIE)
De Laplace
(→Coeficiente de dilatación lineal) |
|||
| Línea 11: | Línea 11: | ||
donde en general esta función podrá ser muy complicada. | donde en general esta función podrá ser muy complicada. | ||
| - | Si consideramos | + | Si consideramos pequeñas dilataciones de una pieza respecto a la longitud <math>L_0</math> que mide cuando la temperatura es <math>t_0</math>, tenemos que en primera aproximación la dilatación de una pieza es proporcional a la propia longitud de la pieza, es decir, si una barra de 1 m se dilata 1&thinp;mm, una de 2 m s dilatará 2 mm. Por ello |
| - | <center><math> | + | <center><math>\frac{\Delta L}{L_0} = f(t_C)</math></center> |
| + | siendo <math>f(t_C)</math> una cierta función de la temperatura, pero no de la longitud de la pieza. Esta función se anula en <math>t_0</math> y si nos separamos poco de esta temperatura podemos hacer una aproximación lineal y admitir que la dilatación es proporcional al incremento de temperatura (si con un incremento de 1°C se dilata 1 mm, con 2°C se dilata 2 mm), por lo que podemos escribir | ||
| + | |||
| + | <center><math>f(t_C)\simeq \alpha \Delta t_C</math></center> | ||
| + | |||
| + | o, equivalentemente | ||
| + | |||
| + | <center><math>\frac{1}{L}\frac{\Delta L}{\Delta t_C} = \alpha</math></center> | ||
| + | |||
| + | y | ||
| + | |||
| + | <center><math>L(t_C)=L_0+\Delta L \simeq L_0(1+\alpha(t_C-t_0))\,</math></center> | ||
| + | |||
| + | El factor <math>\alpha</math> es el denominado coeficiente de dilatación lineal. Rigurosamente se define empleando derivadas en lugar de incrementos | ||
| + | |||
| + | <center><math>\alpha \equiv \frac{1}{L}\,\frac{\mathrm{d}L}{\mathrm{d}t_C}</math></center> | ||
| + | |||
| + | Las unidades en que se mide <math>\alpha</math> en el SI son <math>K^{-1}</math> (aunque, dado que se define a partir de incrementos, también pueden emplearse <math>(^\circ\mathrm{C})^{-1}</math> | ||
==Coeficiente de dilatación superficial y volumétrico== | ==Coeficiente de dilatación superficial y volumétrico== | ||
Revisión de 14:10 12 feb 2012
Contenido |
1 Introducción
Una de las propiedades termométricas de uso más frecuente es la dilatación o contracción de una columna de un líquido (mercurio o alcohol) o de una fina metálica.
Estos termómetros se basan en el hecho empírico de que la longitud de una porción de material cambia con la temperatura (normalmente expandiéndose al aumentar ésta). La causa microscópica de este fenómeno es la variación de la energía cinética de los átomos del material, lo que provoca un cambio en las distancias de equilibrio entre los diferentes átomos, y que se traduce en una dilatación (o contracción) macroscópica.
2 Coeficiente de dilatación lineal
Considerando solo variables macroscópicas, la longitud de una porción de material será una función de la temperatura
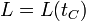
donde en general esta función podrá ser muy complicada.
Si consideramos pequeñas dilataciones de una pieza respecto a la longitud L0 que mide cuando la temperatura es t0, tenemos que en primera aproximación la dilatación de una pieza es proporcional a la propia longitud de la pieza, es decir, si una barra de 1 m se dilata 1&thinp;mm, una de 2 m s dilatará 2 mm. Por ello
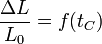
siendo f(tC) una cierta función de la temperatura, pero no de la longitud de la pieza. Esta función se anula en t0 y si nos separamos poco de esta temperatura podemos hacer una aproximación lineal y admitir que la dilatación es proporcional al incremento de temperatura (si con un incremento de 1°C se dilata 1 mm, con 2°C se dilata 2 mm), por lo que podemos escribir
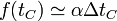
o, equivalentemente
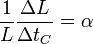
y

El factor α es el denominado coeficiente de dilatación lineal. Rigurosamente se define empleando derivadas en lugar de incrementos
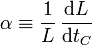
Las unidades en que se mide α en el SI son K − 1 (aunque, dado que se define a partir de incrementos, también pueden emplearse