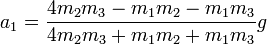Entrar Página Discusión Historial Go to the site toolbox

Doble máquina de Atwood

De Laplace

(Diferencias entre revisiones)
(→Solución)
(→Solución)
Línea 9: Línea 9:
Considerando los diagramas de cuerpo libre, tenemos lo siguiente:
Considerando los diagramas de cuerpo libre, tenemos lo siguiente:
-
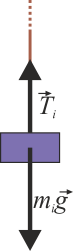
Sobre la masa <math>m_1</math> actúa la tensión de la cuerda y su peso, por lo que
+
[[Archivo:doble-atwood-mi.png|left]] Sobre la masa <math>m_1</math> actúa la tensión de la cuerda y su peso, por lo que
<center><math>\vec{T}_1 + m_1\vec{g} = m_1\vec{a}_1</math></center>
<center><math>\vec{T}_1 + m_1\vec{g} = m_1\vec{a}_1</math></center>
Línea 16: Línea 16:
<center><math>T_1-m_1g = m_1a_1\,</math></center>
<center><math>T_1-m_1g = m_1a_1\,</math></center>
 +
 +
La aceleración de la masa 1 (y análogamente la de las otras dos masas) es la segunda derivada temporal de posición, que en el caso del movimiento vertical se reduce a
 +
 +
<center><math>a_1 = \frac{\mathrm{d}z_1}{\mathrm{d}t^2}</math></center>
Para la masa 2 tenemos, de manera análoga
Para la masa 2 tenemos, de manera análoga
Línea 31: Línea 35:
Ahora bien, ¿cómo se relacionan estas dos tensiones con <math>T_1</math>, la tensión de la otra cuerda. Para obtenerlo escribimos la ecuación de movimiento para esta polea, para la que suponemos provisionalmente una masa <math>m_0</math>. Sobre esta polea actúan tres tensiones además del peso, siendo una de ellas igual a la que actúa sobre la masa 1.
Ahora bien, ¿cómo se relacionan estas dos tensiones con <math>T_1</math>, la tensión de la otra cuerda. Para obtenerlo escribimos la ecuación de movimiento para esta polea, para la que suponemos provisionalmente una masa <math>m_0</math>. Sobre esta polea actúan tres tensiones además del peso, siendo una de ellas igual a la que actúa sobre la masa 1.
-
<center><math>T_1 - T_2-T_3 - m_0g = m_0a_0\,</math></center>
+
<center><math>T_0 - T_2-T_3 - m_0g = m_0a_0\,</math></center>
Al ser una polea ideal, su masa es nula, por lo que nos queda la relación de equilibrio
Al ser una polea ideal, su masa es nula, por lo que nos queda la relación de equilibrio
-
<center><math>T_1 = T_2 + T_3 = 2T_2\,</math></center>
+
<center><math>T_0 - T_2 - T_3 = 0\qquad\Rightarrow\qquad T_0=2T_2\,</math></center>
 +
 
 +
Como por otro lado, esta polea y la masa 1 está unidas por la misma cuerda
 +
 
 +
<center><math>T_1=T_0=2T_2\,</math></center>
Las cuerdas son inextensibles, lo que permite relacionar las aceleraciones. En este caso no es cierto que la aceleración con la que sube <math>m_2</math> sea la misma que con la que baja <math>m_3</math> ya que ambas penden de un punto que también se mueve aceleradamente.
Las cuerdas son inextensibles, lo que permite relacionar las aceleraciones. En este caso no es cierto que la aceleración con la que sube <math>m_2</math> sea la misma que con la que baja <math>m_3</math> ya que ambas penden de un punto que también se mueve aceleradamente.

Revisión de 18:04 24 nov 2011

1 Enunciado

La doble máquina de Atwood de la figura está formada por tres masas unidas a través de dos cuerdas ideales (inextensibles y sin masa) y dos poleas también ideales (de masa despreciable y sin rozamiento). Determine la aceleración de cada una de las masas, así como las tensiones de las dos cuerdas.

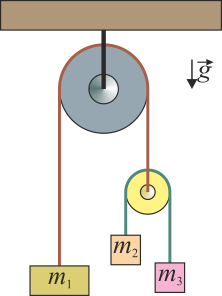
Archivo:doble-maquina-atwood.png

2 Solución

Considerando los diagramas de cuerpo libre, tenemos lo siguiente:

Sobre la masa m1 actúa la tensión de la cuerda y su peso, por lo que
\vec{T}_1 + m_1\vec{g} = m_1\vec{a}_1

dado que todas las fuerzas y aceleraciones en este problema son verticales, podemos usar cantidades escalares y escribir

T_1-m_1g = m_1a_1\,

La aceleración de la masa 1 (y análogamente la de las otras dos masas) es la segunda derivada temporal de posición, que en el caso del movimiento vertical se reduce a

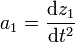
a_1 = \frac{\mathrm{d}z_1}{\mathrm{d}t^2}

Para la masa 2 tenemos, de manera análoga

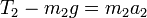
T_2 - m_2g = m_2a_2\,

y para la 3

T_3 - m_3g = m_3a_3\,

Por el hecho de tratarse de cuerdas ideales, inextensibles y sin masa, la tensión en la cuerda que ata las masas 2 y 3 es la misma en todos sus puntos, por lo que

T_2 = T_3\,

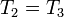
Ahora bien, ¿cómo se relacionan estas dos tensiones con T1, la tensión de la otra cuerda. Para obtenerlo escribimos la ecuación de movimiento para esta polea, para la que suponemos provisionalmente una masa m0. Sobre esta polea actúan tres tensiones además del peso, siendo una de ellas igual a la que actúa sobre la masa 1.

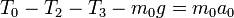
T_0 - T_2-T_3 - m_0g = m_0a_0\,

Al ser una polea ideal, su masa es nula, por lo que nos queda la relación de equilibrio

T_0 - T_2 - T_3 = 0\qquad\Rightarrow\qquad T_0=2T_2\,

Como por otro lado, esta polea y la masa 1 está unidas por la misma cuerda

T_1=T_0=2T_2\,

Las cuerdas son inextensibles, lo que permite relacionar las aceleraciones. En este caso no es cierto que la aceleración con la que sube m2 sea la misma que con la que baja m3 ya que ambas penden de un punto que también se mueve aceleradamente.

Si la polea superior se encuentra a una altura H respecto al suelo, las masas se encuentran a alturas z1, z2 y z3 respectivamente, y la polea pequeña a una altura z_0, la longitud de la cuerda que la une con la masa 1 es

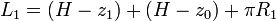
L_1 = (H-z_1) + (H-z_0)+\pi R_1\,

Derivando esta ecuación dos veces respecto al tiempo

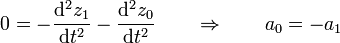
0=-\frac{\mathrm{d}^2z_1}{\mathrm{d}t^2}-\frac{\mathrm{d}^2z_0}{\mathrm{d}t^2}\qquad\Rightarrow\qquad a_0 = -a_1

Por su parte la longitud de la cuerda que pasa por la polea pequeña vale

L_2 = (z_0-z_2)+(z_0-z_3)+\pi R\,

que tras derivar nos da

2a_0 = a_2+a_3\,

Ya tenemos información suficiente para hallar las aceleraciones. Tenemos el sistema

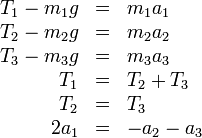
\begin{array}{rcl} T_1-m_1g & = & m_1a_1\\ T_2-m_2g & = & m_2a_2\\ T_3-m_3g & = & m_3a_3\\ T_1 & = & T_2+T_3\\ T_2 & = & T_3\\ 2a_1 & = & -a_2-a_3 \end{array}

Despejando y sustituyendo llegamos a los resultados

a_1=\frac{4m_2m_3-m_1m_2-m_1m_3}{4m_2m_3+m_1m_2+m_1m_3}g        a_2=\frac{3m_1m_3-m_1m_2-4m_2m_3}{4m_2m_3+m_1m_2+m_1m_3}g        a_3=\frac{3m_1m_2-m_1m_3-4m_2m_3}{4m_2m_3+m_1m_2+m_1m_3}g
Obtenido de "http://tesla.us.es/wiki/index.php/Doble_m%C3%A1quina_de_Atwood"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace