Movimiento sinusoidal cuadrático

De Laplace

(Diferencias entre revisiones)

Revisión de 20:04 17 oct 2011

1 Enunciado

Una partícula oscila según la ley

$x(t) = A\,\mathrm{sen}^2(\Omega t)$

Pruebe que se trata de un movimiento armónico simple. ¿Cuál es su posición de equilibrio?
¿Cuánto valen la frecuencia, periodo y amplitud de este movimiento?

2 Solución

Para ver que se trata de un movimiento armónico podemos analizar la propia solución o comprobar si verifica la ecuación del oscilador armónico.

Hay que destacar que el hecho de que se trate de una función oscilante o periódica no equivale a que sea un movimiento armónico. Por ejemplo, si el exponente fuera un cubo en vez de un cuadrado, no se trataría de un m.a.s. Para que sea armónico debe verificarse la ecuación de movimiento

$a = \ddot{x}=-\omega^2(x-x_c)$

Derivamos entonces nuestra función, para ver si se cumple una ecuación de este tipo. Primero hallamos la velocidad

$v = \dot{x} = 2A\Omega\cos(\Omega t)\mathrm{sen}(\Omega t)$

y derivando de nuevo la aceleración

$a = \ddot{x} = 2A\Omega^2\left(\cos^2(\Omega t)-\mathrm{sen}^2(\Omega t)\right)$

Aplicando la relación

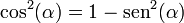
$\cos^2(\alpha) = 1 - \mathrm{sen}^2(\alpha)\,$

nos queda

$a = 2A\Omega^2\left(1-2\mathrm{sen}^2(\Omega t)\right) = -4\Omega^2\left(x-\frac{A}{2}\right)$

Esta sí es la ecuación de un oscilador armónico, si hacemos

$\omega^2 = 4\Omega^2 \qquad\Rightarrow\qquad \omega = 2\Omega\qquad\qquad x_c = \frac{A}{2}$

@@ Línea 28: / Línea 28: @@
 nos queda
-<center><math>a = 2A\Omega^2(1-2\mathrm{sen}^2(\Omega t)} = -4\Omega^2\left(x-\frac{A}{2}\right)</math></center>
+<center><math>a = 2A\Omega^2\left(1-2\mathrm{sen}^2(\Omega t)\right) = -4\Omega^2\left(x-\frac{A}{2}\right)</math></center>
 Esta sí es la ecuación de un oscilador armónico, si hacemos

Movimiento sinusoidal cuadrático

De Laplace

Revisión de 20:04 17 oct 2011

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES