Entrar Página Discusión Historial Go to the site toolbox

Campo de un cable bimetalico

De Laplace

(Diferencias entre revisiones)
(Página creada con '==Enunciado== Entre los distintos tipos de cable empleados en la industria, se encuentra el de ''aluminio revestido de cobre''. Está formado por un núcleo de aluminio de radio…')
(→Campo magnético)
Línea 40: Línea 40:
==Campo magnético==
==Campo magnético==
 +
El valor del campo magnético lo obtenemos aplicando la ley de Ampère. Dado que tenemos medios materiales, emplearemos la versión correspondiente al campo <math>\mathbf{H}</math>
 +
 +
<center><math>\oint_\Gamma \mathbf{H}\cdot\mathrm{d}\mathbf{r} = I = \int_S\mathbf{J}\cdot\mathrm{d}\mathbf{S}</math></center>
 +
 +
donde I es la corriente libre que traviesa una superficie S apoyada en la curva &Gamma;
 +
 +
Por la simetría del sistema, el campo magnético debe ir en la dirección de <math>\mathbf{u}_{\varphi}</math> y depender exclusivamente de la distancia al eje del cable
 +
 +
\mathbf{H} = H(\rho)\mathbf{u}_{\varphi}
 +
 +
La circulación de este campo a lo largo de una circunferencia concéntrica con el eje es
 +
\[
 +
\oint \mathbf{H}{\cdot}\mathrm{d}\mathbf{r} = 2\pi\rho H
 +
\]
 +
 +
De acuerdo con la ley de Ampère, esta circulación debe ser igual  la corriente que atraviesa una superficie apoyada en la curva. Tenemos tres casos, dependiendo de <math>\rho</math>: que estemos en el núcleo de aluminio, en la corteza de cobre o en el exterior del cable.
 +
 +
En el núcleo de aluminio, la corriente que atraviesa este círculo es la integral de <math>\mathbf{J}_1</math> sobre éste
 +
 +
<center><math>2\pi\rho H = \int\mathbf{J}{\cdot}\mathrm{d}\mathbf{S} = \int_0^{2\pi}\!\!\int_0^\rho J_1\rho\,\mathrm{d}\rho\,\mathrm{d}\varphi = \pi \rho^2 J_1</math></center>
 +
 +
resultando el campo magnético <math>\mathbf{H}</math>
 +
 +
<center><math>\mathbf{H} = \frac{J_1\rho}{2}\mathbf{u}_{\varphi}= \frac{I \sigma_1\rho \mathbf{u}_{\varphi}}
 +
{2\pi(\sigma_1 a^2+\sigma_2(b^2-a^2))}\qquad (\rho< a)</math></center>
 +
 +
El campo magnético \mathbf{B} lo obtenemos multiplicando por la permeabilidad del aluminio
 +
 +
<center><math>\mathbf{B}=\mu_1\mathbf{H} = \frac{\mu_1 J_1\rho}{2}\mathbf{u}_{\varphi}= \frac{\mu_1 I \sigma_1\rho \mathbf{u}_{\varphi}}
 +
{2\pi(\sigma_1 a^2+\sigma_2(b^2-a^2))}\qquad (\rho< a)</math></center>
 +
 +
En el recubrimiento de cobre, la corriente que atraviesa el círculo incluye tanto la del aluminio como una parte de la que va por la propia corteza
 +
 +
<center><math>2\pi\rho H = \int\mathbf{J}{\cdot}\mathrm{d}\mathbf{S} = \mu_0\left(
 +
\int_0^{2\pi}\!\!\int_0^a J_1\rho\,\mathrm{d}\rho\,\mathrm{d}\varphi + \int_0^{2\pi}\!\!\int_a^\rho J_2\rho\,\mathrm{d}\rho\,\mathrm{d}\varphi\right)
 +
=\pi\left(J_1 a^2+J_2(\rho^2-a^2)\right)</math></center>
 +
 +
de donde
 +
 +
<center><math>\mathbf{H} = \frac{(J_1 a^2 + J_2(\rho^2-a^2))}{2\rho}\mathbf{u}_{\varphi}=
 +
\frac{I (\sigma_1 a^2 + \sigma_2(\rho^2-a^2))\mathbf{u}_{\varphi}}{2\pi\rho(\sigma_1
 +
a^2+\sigma_2(b^2-a^2))}\qquad (a<\rho<b)
 +
</math></center>
 +
 +
Multiplicando ahora por la permeabilidad del cobre
 +
 +
<center><math>\mathbf{B} = \frac{\mu_2(J_1 a^2 + J_2(\rho^2-a^2))}{2\rho}\mathbf{u}_{\varphi}=
 +
\frac{\mu_2 I (\sigma_1 a^2 + \sigma_2(\rho^2-a^2))\mathbf{u}_{\varphi}}{2\pi\rho(\sigma_1
 +
a^2+\sigma_2(b^2-a^2))}\qquad (a<\rho<b)
 +
</math></center>
 +
 +
Por último, en el exterior, la corriente abarcada es la totalidad
 +
 +
<center><math>2\pi\rho H = I \quad\Rightarrow\qquad \mathbf{H} = \frac{I\mathbf{u}_{\varphi}}{2\pi\rho}\qquad (\rho>b)
 +
</math></center>
 +
 +
siendo ahora la permeabilidad la del vacío
 +
 +
<center><math>\mathbf{B} = \frac{\mu_0 I\mathbf{u}_{\varphi}}{2\pi\rho}\qquad (\rho>b)
 +
</math></center>
 +
 +
Resulta un campo magnético que varía de forma continua, siendo nulo justo en el centro del cable, creciendo linealmente desde ahí hasta la
 +
interfaz aluminio/cobre, en la que alcanza el valor de <math>B_1=3.4\,\mathrm{mT}</math>. A partir de ahí sigue creciendo como combinación de una función lineal y de una que va como <math>1/\rho</math>. El valor máximo lo alcanza en la superficie exterior del cable, donde vale
 +
 +
<center><math>B(\rho=b) = \frac{\mu_0I}{2\pi b}= 6.7\,\mathrm{mT}</math></center>
 +
 +
En el exterior del cable, el campo disminuye con la inversa de la distancia, de forma equivalente a que toda la corriente estuviera concentrada en el eje del cable.
 +
[[Categoría:Problemas de materiales magnéticos]]
[[Categoría:Problemas de materiales magnéticos]]

Revisión de 14:53 9 jun 2011

1 Enunciado

Entre los distintos tipos de cable empleados en la industria, se encuentra el de aluminio revestido de cobre. Está formado por un núcleo de aluminio de radio a (suponga a = 2mm), rodeado por una capa de cobre, de radio exterior b (sea 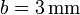b= 3\,\mathrm{mm}).

Halle el campo magnético producido por el cable, tanto en su interior como su exterior, cuando por él circula una corriente 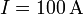I=100\,\mathrm{A}. ¿Cuál es el valor máximo del campo magnético? ¿Dónde se alcanza?

Image:cableconnucleo.gif

2 Densidad de corriente

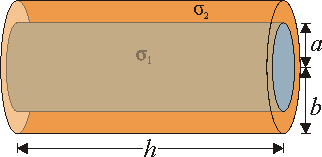
La corriente I se distribuye por todo el cable, pero no uniformemente, debido a la diferente conductividad de los dos materiales.

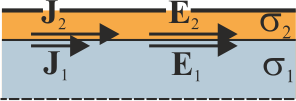
Al ser la interfaz paralela a las líneas de corriente y de campo, la continuidad en la componente tangencial de \mathbf{E} implica que el campo eléctrico tiene el mismo valor en el aluminio y en el cobre.

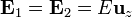
\mathbf{E}_1=\mathbf{E}_2=E\mathbf{u}_{z}

La densidad de corriente, en cambio, será mayor en el de mayor conductividad, el cobre

\mathbf{J}_1=\sigma_1E\mathbf{u}_{z}\qquad \mathbf{J}_2=\sigma_2E\mathbf{u}_{z}

El valor de E lo obtenemos de la corriente total, que es suma de la que circula por el cobre y por el aluminio

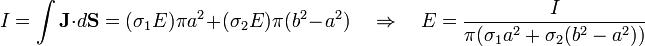
I = \int\mathbf{J}{\cdot}d\mathbf{S} = (\sigma_1 E)\pi a^2 + (\sigma_2 E)\pi(b^2-a^2) \quad\Rightarrow\quad E=\frac{I}{\pi(\sigma_1 a^2+\sigma_2(b^2-a^2))}

y de aquí obtenemos la densidad de corriente que fluye por cada material

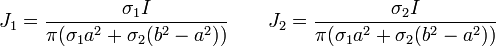
J_1=\frac{\sigma_1 I}{\pi(\sigma_1 a^2+\sigma_2(b^2-a^2))}\qquad J_2=\frac{\sigma_2 I}{\pi(\sigma_1 a^2+\sigma_2(b^2-a^2))}

Los valores numéricos de estas tres cantidades son

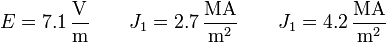
E=7.1\,\frac{\mathrm{V}}{\mathrm{m}}\qquad J_1= 2.7\,\frac{\mathrm{MA}}{\mathrm{m}^2}\qquad J_1= 4.2\,\frac{\mathrm{MA}}{\mathrm{m}^2}

Resulta que por el núcleo de cobre circula el 34% de la corriente mientras que por el recubrimiento de cobre va el 66% restante.

3 Campo magnético

El valor del campo magnético lo obtenemos aplicando la ley de Ampère. Dado que tenemos medios materiales, emplearemos la versión correspondiente al campo \mathbf{H}

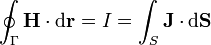
\oint_\Gamma \mathbf{H}\cdot\mathrm{d}\mathbf{r} = I = \int_S\mathbf{J}\cdot\mathrm{d}\mathbf{S}

donde I es la corriente libre que traviesa una superficie S apoyada en la curva Γ

Por la simetría del sistema, el campo magnético debe ir en la dirección de 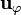\mathbf{u}_{\varphi} y depender exclusivamente de la distancia al eje del cable

\mathbf{H} = H(\rho)\mathbf{u}_{\varphi}

La circulación de este campo a lo largo de una circunferencia concéntrica con el eje es \[ \oint \mathbf{H}{\cdot}\mathrm{d}\mathbf{r} = 2\pi\rho H \]

De acuerdo con la ley de Ampère, esta circulación debe ser igual la corriente que atraviesa una superficie apoyada en la curva. Tenemos tres casos, dependiendo de ρ: que estemos en el núcleo de aluminio, en la corteza de cobre o en el exterior del cable.

En el núcleo de aluminio, la corriente que atraviesa este círculo es la integral de 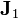\mathbf{J}_1 sobre éste

2\pi\rho H = \int\mathbf{J}{\cdot}\mathrm{d}\mathbf{S} = \int_0^{2\pi}\!\!\int_0^\rho J_1\rho\,\mathrm{d}\rho\,\mathrm{d}\varphi = \pi \rho^2 J_1

resultando el campo magnético \mathbf{H}

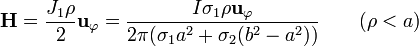
\mathbf{H} = \frac{J_1\rho}{2}\mathbf{u}_{\varphi}= \frac{I \sigma_1\rho \mathbf{u}_{\varphi}} {2\pi(\sigma_1 a^2+\sigma_2(b^2-a^2))}\qquad (\rho< a)

El campo magnético \mathbf{B} lo obtenemos multiplicando por la permeabilidad del aluminio

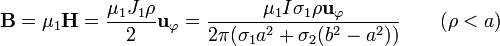
\mathbf{B}=\mu_1\mathbf{H} = \frac{\mu_1 J_1\rho}{2}\mathbf{u}_{\varphi}= \frac{\mu_1 I \sigma_1\rho \mathbf{u}_{\varphi}} {2\pi(\sigma_1 a^2+\sigma_2(b^2-a^2))}\qquad (\rho< a)

En el recubrimiento de cobre, la corriente que atraviesa el círculo incluye tanto la del aluminio como una parte de la que va por la propia corteza

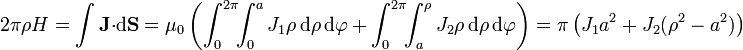
2\pi\rho H = \int\mathbf{J}{\cdot}\mathrm{d}\mathbf{S} = \mu_0\left( \int_0^{2\pi}\!\!\int_0^a J_1\rho\,\mathrm{d}\rho\,\mathrm{d}\varphi + \int_0^{2\pi}\!\!\int_a^\rho J_2\rho\,\mathrm{d}\rho\,\mathrm{d}\varphi\right) =\pi\left(J_1 a^2+J_2(\rho^2-a^2)\right)

de donde

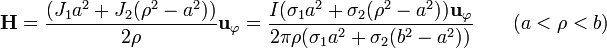
\mathbf{H} = \frac{(J_1 a^2 + J_2(\rho^2-a^2))}{2\rho}\mathbf{u}_{\varphi}= \frac{I (\sigma_1 a^2 + \sigma_2(\rho^2-a^2))\mathbf{u}_{\varphi}}{2\pi\rho(\sigma_1 a^2+\sigma_2(b^2-a^2))}\qquad (a<\rho<b)

Multiplicando ahora por la permeabilidad del cobre

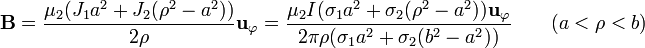
\mathbf{B} = \frac{\mu_2(J_1 a^2 + J_2(\rho^2-a^2))}{2\rho}\mathbf{u}_{\varphi}= \frac{\mu_2 I (\sigma_1 a^2 + \sigma_2(\rho^2-a^2))\mathbf{u}_{\varphi}}{2\pi\rho(\sigma_1 a^2+\sigma_2(b^2-a^2))}\qquad (a<\rho<b)

Por último, en el exterior, la corriente abarcada es la totalidad

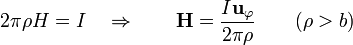
2\pi\rho H = I \quad\Rightarrow\qquad \mathbf{H} = \frac{I\mathbf{u}_{\varphi}}{2\pi\rho}\qquad (\rho>b)

siendo ahora la permeabilidad la del vacío

\mathbf{B} = \frac{\mu_0 I\mathbf{u}_{\varphi}}{2\pi\rho}\qquad (\rho>b)

Resulta un campo magnético que varía de forma continua, siendo nulo justo en el centro del cable, creciendo linealmente desde ahí hasta la interfaz aluminio/cobre, en la que alcanza el valor de 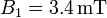B_1=3.4\,\mathrm{mT}. A partir de ahí sigue creciendo como combinación de una función lineal y de una que va como 1 / ρ. El valor máximo lo alcanza en la superficie exterior del cable, donde vale

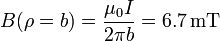
B(\rho=b) = \frac{\mu_0I}{2\pi b}= 6.7\,\mathrm{mT}

En el exterior del cable, el campo disminuye con la inversa de la distancia, de forma equivalente a que toda la corriente estuviera concentrada en el eje del cable.

Obtenido de "http://tesla.us.es/wiki/index.php/Campo_de_un_cable_bimetalico"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace