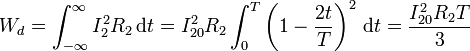Pulso de corriente inducida
De Laplace
(→Corriente inducida) |
|||
| (24 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | == | + | ==Enunciado== |
Por un hilo rectilíneo de gran longitud y resistencia eléctrica <math>R_1</math> circula una corriente variable en el tiempo, tal | Por un hilo rectilíneo de gran longitud y resistencia eléctrica <math>R_1</math> circula una corriente variable en el tiempo, tal | ||
que su valor es | que su valor es | ||
| Línea 12: | Línea 12: | ||
==Carga que recorre el hilo== | ==Carga que recorre el hilo== | ||
| + | [[Archivo:pulso-corriente-hilo.png|right]] | ||
| + | |||
| + | La carga que pasa por una sección del hilo en un tiempo <math>\mathrm{d}t</math> es | ||
| + | |||
| + | <center><math>\mathrm{d}Q=I(t)\,\mathrm{d}t</math></center> | ||
| + | |||
| + | Por lo que la carga total que pasa vale | ||
| + | |||
| + | <center><math>Q= \int_{-\infty}^\infty I(t)\,\mathrm{d}t</math></center> | ||
| + | |||
| + | En este caso, tenemos que la corriente es nula salvo en el intervalo <math>0 < t < T</math> por lo que el cálculo se reduce a | ||
| + | |||
| + | <center><math>Q = \int_0^T I(t)\,\mathrm{d}t = \frac{I_0}{T^2}\int_0^T (tT-t^2)\mathrm{d}t = \frac{I_0}{T^2}\left(\frac{T^3}{2}-\frac{T^3}{3}\right) = \frac{I_0T}{6}</math></center> | ||
| + | |||
==Energía disipada en el hilo== | ==Energía disipada en el hilo== | ||
| + | La energía disipada se calcula de forma análoga a partir de la potencia | ||
| + | |||
| + | <center><math>W_d = \int_0^T I^2R_1\,\mathrm{d}t = \frac{I_0^2R_1}{T^4}\int_0^T (tT-t^2)^2\mathrm{d}t =</math><math>\,\,\frac{I_0^2R_1}{T^4}\int_0^T (t^2T^2-2t^3T+t^4)\mathrm{d}t=\frac{I_0^2R_1}{T^4}\left(\frac{T^5}{3}-2\frac{T^5}{4}+\frac{T^5}{5}\right) = \frac{I_0^2TR_1}{30}</math></center> | ||
| + | |||
==Corriente inducida== | ==Corriente inducida== | ||
| + | [[Archivo:campo-hilo-espira-cuadrada.png|left]] | ||
| + | |||
| + | La corriente inducida la obtenemos por aplicación de la ley de Faraday | ||
| + | |||
| + | <center><math>I_2=-\frac{1}{R_2}\frac{\mathrm{d}\Phi_m}{\mathrm{d}t}</math></center> | ||
| + | |||
| + | El flujo magnético lo calculamos a partir del campo producido por el hilo | ||
| + | |||
| + | <center><math>\mathbf{B}_1=\frac{\mu_0I_1}{2\pi\rho}\mathbf{u}_\varphi</math></center> | ||
| + | |||
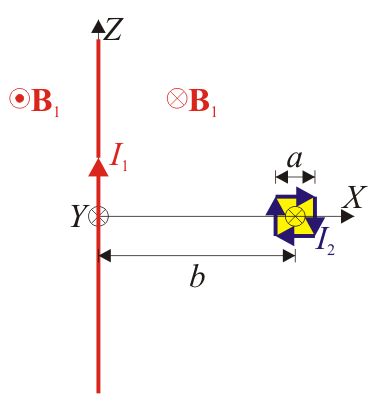
| + | Puesto que la espira es muy pequeña, podemos suponer que <math>\rho = b</math> para todos sus puntos. Asimismo, en la posición de la espira, el campo magnético apunta en la dirección hacia adentro del plano, que es la marcada por <math>\mathbf{u}_y</math>. Por ello | ||
| + | |||
| + | <center><math>\mathbf{B}_1\simeq\frac{\mu_0I_1}{2\pi b}\mathbf{u}_y</math></center> | ||
| + | |||
| + | Tomando un sentido de recorrido de la espira tal que la normal a la superficie es también <math>\mathbf{u}_y</math> nos queda | ||
| + | |||
| + | <center><math>\Phi_m = \int_{S_2}\mathbf{B}_1\cdot\mathrm{d}\mathbf{S}_2 = \frac{\mu_0I_1a^2}{2\pi b}</math></center> | ||
| + | |||
| + | [[Archivo:pulso-corriente-espira.png|right]] | ||
| + | |||
| + | Esta función depende del tiempo porque lo hace la corriente que pasa por el hilo, por ello la corriente inducida es | ||
| + | |||
| + | <center><math>I_2 = -\frac{\mu_0a^2}{2\pi b R_2}\,\frac{\mathrm{d}I_1}{\mathrm{d}t}</math></center> | ||
| + | |||
| + | Sustituyendo la expresión de <math>I_1</math> | ||
| + | |||
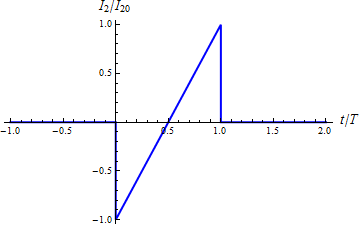
| + | <center><math>I_2 = \begin{cases}\displaystyle -I_{20}\left(1-\frac{2t}{T}\right) & 0 < t < T \\ & \\ 0 & t<0\ \mathrm{o}\ t>T\end{cases}\qquad I_{20}=\frac{\mu_0a^2I_0}{2\pi b R_2T}</math></center> | ||
| + | |||
| + | Esta función es nula en todo instante salvo en el intervalo <math>(0,T)</math>, en el cual tiene forma de rampa. Inicialmente el flujo está aumentando, por lo que la corriente inducida tiende a disminuirlo. Posteriormente el flujo disminuye, por lo que la corriente tiende a aumentarlo. | ||
| + | |||
==Carga que recorre la espira== | ==Carga que recorre la espira== | ||
| + | La carga se calcula de la misma manera que en el primer apartado | ||
| + | |||
| + | <center><math>Q_2 = \int_{-\infty}^{\infty}I_2\,\mathrm{d}t</math></center> | ||
| + | |||
| + | De la simetría impar de la función <math>I_2(t)</math> respecto al centro del periodo, es fácil ver que esta integral va a ser nula. | ||
| + | |||
| + | Es más directo y general hallarlo de la forma siguiente | ||
| + | |||
| + | <center><math>Q_2 = \int_{-\infty}^{\infty}I_2\,\mathrm{d}t = -\frac{1}{R_2}\int_{-\infty}^{\infty}\frac{\mathrm{d}\Phi_m}{\mathrm{d}t}\,\mathrm{d}t = -\frac{\Delta\Phi_m}{R_2}</math></center> | ||
| + | |||
| + | siendo <math>\Delta\Phi_m</math> el incremento de flujo entre el instante final y el inicial. Puesto que tanto en <math>t\to+\infty</math> como en <math>t\to-\infty</math> el flujo magnético es nulo, deducimos que | ||
| + | |||
| + | <center><math>Q_2 = -\frac{\Delta\Phi_m}{R_2} = 0</math></center> | ||
| + | |||
==Energía disipada en la espira== | ==Energía disipada en la espira== | ||
| + | La energía disipada en la espira, en cambio, no es nula. Aplicando de nuevo la ley de Joule | ||
| + | |||
| + | <center><math>W_d = \int_{-\infty}^\infty I_2^2R_2\,\mathrm{d}t=I_{20}^2R_2\int_0^T\left(1-\frac{2t}{T}\right)^2\,\mathrm{d}t = \frac{I_{20}^2R_2T}{3}</math></center> | ||
[[Categoría:Problemas de corriente eléctrica]] | [[Categoría:Problemas de corriente eléctrica]] | ||
[[Categoría:Problemas de inducción electromagnética]] | [[Categoría:Problemas de inducción electromagnética]] | ||
última version al 09:10 1 jun 2011
Contenido |
1 Enunciado
Por un hilo rectilíneo de gran longitud y resistencia eléctrica R1 circula una corriente variable en el tiempo, tal que su valor es
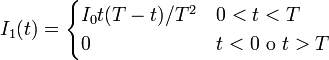
- Halle la carga que pasa por un punto del hilo entre
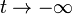 y
y 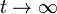 .
.
- Calcule la energía disipada en el cable en el mismo tiempo.
- Junto al cable y coplanaria con él se encuentra una pequeña espira cuadrada de lado a con su centro situado a una distancia b (
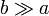 ) del hilo. Esta espira posee resistencia R2 y autoinducción despreciable. Calcule la corriente inducida en esta espira como función del tiempo.
) del hilo. Esta espira posee resistencia R2 y autoinducción despreciable. Calcule la corriente inducida en esta espira como función del tiempo.
- Halle la carga que pasa por un punto de la espira entre
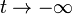 y
y 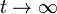 .
.
- Calcule la energía disipada en la espira en el mismo tiempo.
2 Carga que recorre el hilo
La carga que pasa por una sección del hilo en un tiempo dt es
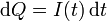
Por lo que la carga total que pasa vale
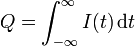
En este caso, tenemos que la corriente es nula salvo en el intervalo 0 < t < T por lo que el cálculo se reduce a
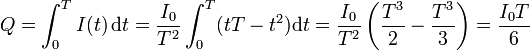
3 Energía disipada en el hilo
La energía disipada se calcula de forma análoga a partir de la potencia
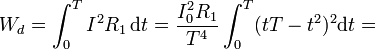
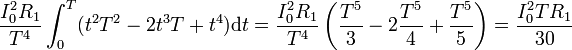
4 Corriente inducida
La corriente inducida la obtenemos por aplicación de la ley de Faraday
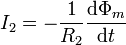
El flujo magnético lo calculamos a partir del campo producido por el hilo
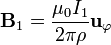
Puesto que la espira es muy pequeña, podemos suponer que ρ = b para todos sus puntos. Asimismo, en la posición de la espira, el campo magnético apunta en la dirección hacia adentro del plano, que es la marcada por 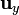 . Por ello
. Por ello
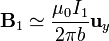
Tomando un sentido de recorrido de la espira tal que la normal a la superficie es también 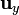 nos queda
nos queda
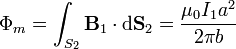
Esta función depende del tiempo porque lo hace la corriente que pasa por el hilo, por ello la corriente inducida es
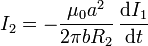
Sustituyendo la expresión de I1
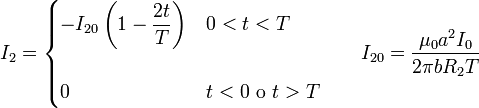
Esta función es nula en todo instante salvo en el intervalo (0,T), en el cual tiene forma de rampa. Inicialmente el flujo está aumentando, por lo que la corriente inducida tiende a disminuirlo. Posteriormente el flujo disminuye, por lo que la corriente tiende a aumentarlo.
5 Carga que recorre la espira
La carga se calcula de la misma manera que en el primer apartado
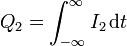
De la simetría impar de la función I2(t) respecto al centro del periodo, es fácil ver que esta integral va a ser nula.
Es más directo y general hallarlo de la forma siguiente
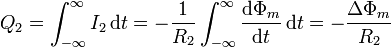
siendo ΔΦm el incremento de flujo entre el instante final y el inicial. Puesto que tanto en 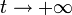 como en
como en 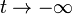 el flujo magnético es nulo, deducimos que
el flujo magnético es nulo, deducimos que
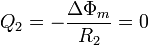
6 Energía disipada en la espira
La energía disipada en la espira, en cambio, no es nula. Aplicando de nuevo la ley de Joule