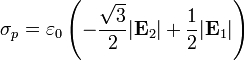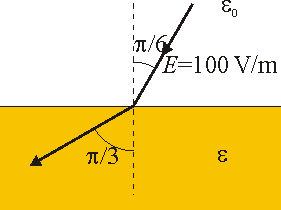Refracción de un campo eléctrico
De Laplace
(→Módulo del campo) |
|||
| Línea 55: | Línea 55: | ||
El módulo del campo podemos hallar de la continuidad de la componente tangencial del campo eléctrico | El módulo del campo podemos hallar de la continuidad de la componente tangencial del campo eléctrico | ||
| - | <center><math>|\mathbf{E}_1| = \frac{1}{\sqrt{3}}|\mathbf{E} | + | <center><math>|\mathbf{E}_1| = \frac{1}{\sqrt{3}}|\mathbf{E}_2| = 58\,\frac{\mathrm{V}}{\mathrm{m}}</math></center> |
Alternativamente, puede hallarse la permitividad una vez conocido el módulo del campo, a partir de la continuidad de la componente normal del desplazamiento. | Alternativamente, puede hallarse la permitividad una vez conocido el módulo del campo, a partir de la continuidad de la componente normal del desplazamiento. | ||
Revisión de 21:03 3 mar 2011
Contenido |
1 Enunciado
- La permitividad relativa del medio.
- El módulo del campo en el interior del material.
- La densidad de carga de polarización en la frontera.
- El salto en la componente tangencial de
.
2 Introducción
Este problema se reduce a aplicar las condiciones de salto en la interfaz entre el dieléctrico y el vacío
![\mathbf{n}\cdot[\mathbf{D}]=\sigma_l =0](/wiki/images/math/d/c/d/dcdfc992390471d96423f4d6eda8844c.png)
![\mathbf{n}\times[\mathbf{E}]=\mathbf{0}](/wiki/images/math/6/d/9/6d9a6f945a9f8273282ed8720257a0ba.png)
donde la densidad de carga libre es nula por tratarse de un dieléctrico ideal del que no se nos dice que esté cargado.
Si separamos cada campo en una componente normal a la superficie y una tangencial a ella, queda, por lado
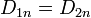
siendo 1 el dieléctrico y 2 el vacío. En términos del campo eléctrico, esta condición es
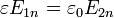
La condición de continuidad de la componente tangencial del campo eléctrico se expresa
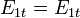
A su vez, para el dieléctrico tenemos, de acuerdo con la figura
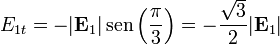
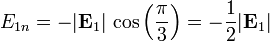
y para el vacío
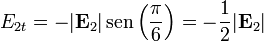
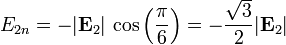
Llevando esto a las dos condiciones de salto queda, para la componente normal
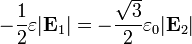
y para la tangencial
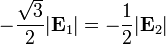
2.1 Permitividad relativa
Dividiendo una igualdad por la otra obtenemos
lo que nos da la permitividad relativa
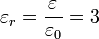
2.2 Módulo del campo
El módulo del campo podemos hallar de la continuidad de la componente tangencial del campo eléctrico
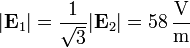
Alternativamente, puede hallarse la permitividad una vez conocido el módulo del campo, a partir de la continuidad de la componente normal del desplazamiento.
3 Carga de polarización
La polarización en un medio lineal verifica
y la carga de polarización en la interfaz es
![\sigma_p = -\mathbf{n}\cdot[\mathbf{P}] = -\overbrace{\mathbf{n}\cdot[\mathbf{D}]}^{=0}+\varepsilon_0\mathbf{n}\cdot[\mathbf{E}]=\varepsilon_0(E_{2n}-E_{1n})](/wiki/images/math/1/2/0/120d8e9d58e022681b86fa0bf3661ae0.png)
En términos de los módulos
