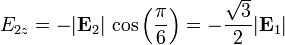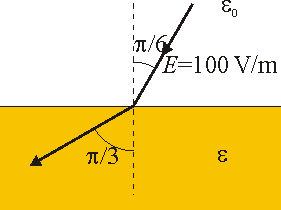Refracción de un campo eléctrico

De Laplace

Revisión de 20:15 3 mar 2011 (ver código fuente) Antonio (Discusión | contribuciones) ← Edición más antigua		Revisión de 20:35 3 mar 2011 (ver código fuente) Antonio (Discusión | contribuciones) Edición más nueva →
Línea 8:		Línea 8:
	==Introducción==		==Introducción==
		+	Este problema se reduce a aplicar las condiciones de salto en la interfaz entre el dieléctrico y el vacío
		+
		+	<center><math>\mathbf{n}\cdot[\mathbf{D}]=\sigma_l =0</math>{{qquad}}{{qquad}}<math>\mathbf{n}\times[\mathbf{E}]=\mathbf{0}</math></center>
		+
		+	donde la densidad de carga libre es nula por tratarse de un dieléctrico ideal del que no se nos dice que esté cargado.
		+
		+	Tomando un sistema de ejes en el que el campo se encuentra en el plano XZ, siendo el eje X el tangente a la superficie y el Z el normal a ella, tenemos que la condición de continuidad en la componente normal del vector desplazamiento  equivale a
		+
		+	<center><math>D_{z1}=D_{z2}\,</math></center>
		+
		+	siendo 1 el dieléctrico y 2 el vacío. En términos del campo eléctrico, esta condición es
		+
		+	<center><math>\varepsilon E_{z1}=\varepsilon_0E_{z2}</math></center>
		+
		+	La condición de continuidad de la componente tangencial del campo eléctrico se expresa
		+
		+	<center><math>E_{x1}=E_{x2}\,</math></center>
		+
		+	A su vez, para el dieléctrico tenemos, de acuerdo con la figura
		+
		+	<center><math>E_{1x} = -|\mathbf{E}_1|\,\mathrm{sen}\left(\frac{\pi}{3}\right) = -\frac{\sqrt{3}}{2}|\mathbf{E}_1|</math>{{qquad}}{{qquad}}<math>E_{1z} = -|\mathbf{E}_1|\,\cos\left(\frac{\pi}{3}\right) = -\frac{1}{2}|\mathbf{E}_1|</math></center>
		+
		+	y para el vacío
		+
		+	<center><math>E_{2x} = -|\mathbf{E}_2|\,\mathrm{sen}\left(\frac{\pi}{6}\right) = -\frac{1}{2}|\mathbf{E}_1|</math>{{qquad}}{{qquad}}<math>E_{2z} = -|\mathbf{E}_2|\,\cos\left(\frac{\pi}{6}\right) = -\frac{\sqrt{3}}{2}|\mathbf{E}_1|</math></center>
		+
		+
		+
		+
		+
	==Permitividad relativa==		==Permitividad relativa==
	==Módulo del campo==		==Módulo del campo==

---

Revisión de 20:35 3 mar 2011

Contenido 1 Enunciado 2 Introducción 3 Permitividad relativa 4 Módulo del campo 5 Carga de polarización 6 Salto en el desplazamiento

1 Enunciado

El campo eléctrico en el exterior de un dieléctrico tiene por módulo 100 V/m y forma un ángulo π / 6 con la normal a la superficie. El campo en el interior del medio forma un ángulo π / 3 con la normal. Halle:

1. La permitividad relativa del medio.
2. El módulo del campo en el interior del material.
3. La densidad de carga de polarización en la frontera.
4. El salto en la componente tangencial de .

2 Introducción

Este problema se reduce a aplicar las condiciones de salto en la interfaz entre el dieléctrico y el vacío

        

donde la densidad de carga libre es nula por tratarse de un dieléctrico ideal del que no se nos dice que esté cargado.

Tomando un sistema de ejes en el que el campo se encuentra en el plano XZ, siendo el eje X el tangente a la superficie y el Z el normal a ella, tenemos que la condición de continuidad en la componente normal del vector desplazamiento equivale a

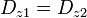
siendo 1 el dieléctrico y 2 el vacío. En términos del campo eléctrico, esta condición es

La condición de continuidad de la componente tangencial del campo eléctrico se expresa

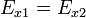
A su vez, para el dieléctrico tenemos, de acuerdo con la figura

        

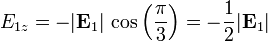
y para el vacío

        

3 Permitividad relativa

4 Módulo del campo

5 Carga de polarización

6 Salto en el desplazamiento