Entrar Página Discusión Historial Go to the site toolbox

Aro con deslizador (G.I.A.)

De Laplace

(Diferencias entre revisiones)
(→Cálculo de vA21 y vC21)
(→Base y ruleta del movimiento {21})
Línea 112: Línea 112:
</math>
</math>
</center>
</center>
 +
Esta curva está descrita en función del parámetro <math>\theta </math>. Durante el movimiento, este ángulo va variando en el tiempo. Para encontrar la expresión de la curva que describe hemos de eliminar el parámetro. Tenemos
 +
<center>
 +
<math>
 +
\vec{r}^{I_{21}}_{21} =
 +
\left\{
 +
\begin{array}{l}
 +
x^{I_{21}}_{21} = 2\,R\,\mathrm{sen}\,\theta \\ \\
 +
y^{I_{21}}_{21} = 2\,R\,\cos\theta
 +
\\ \\
 +
z^{I_{21}}_{21} = 0
 +
\end{array}
 +
\right.
 +
</math>
 +
</center>
 +
Observando las expresiones de las componentes en <math>X_1 </math> e <math>Y_1 </math> vemos que
 +
<center>
 +
<math>
 +
\left(x^{I_{21}}_{21}\right)^2 + \left(y^{I_{21}}_{21}\right)^2 =
 +
4\,R^2\,\mathrm{sen}^2\theta + 4\,R^2\,\cos^2\theta = (2\,R)^2
 +
</math>
 +
</center>
 +
Las ecuaciones implícitas de la base son
 +
<center>
 +
<math>
 +
\left(x^{I_{21}}_{21}\right)^2 + \left(y^{I_{21}}_{21}\right)^2 = (2\,R)^2
 +
\qquad\qquad
 +
z^{I_{21}}_{21} = 0
 +
</math>
 +
</center>
 +
Esto es una circunferencia de radio <math>2R  </math> y centro en el punto <math>O </math>.

Revisión de 23:06 29 dic 2010

Contenido

1 Enunciado

Sea un aro de centro C y radio R (sólido "2") que se mueve, en un plano fijo OX1Y1 (sólido "1"), de tal modo que está obligado a deslizar en todo instante por un pasador giratorio situado en el punto O, y además se halla articulado en su punto A a un deslizador que se mueve siempre sobre el eje horizontal OX1 (ver figura). Con carácter auxiliar, se define el sistema de ejes OX2Y2 (sólido "2") solidario con el aro en su movimiento. Se pide:

  1. Determinar gráfica y analíticamente la posición del C.I.R. del movimiento {21}.
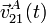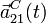  2. Sabiendo que el ángulo θ, que forman los ejes OX1 y AX2, verifica la ley horaria θ(t) = ωt (donde ω es una constante conocida), calcular \vec{v}_{21}^A(t) y \vec{a}_{21}^C(t).

2 Solución

2.1 Determinación gráfica del CIR

Vayamos primero con la determinación gráfica. Tenemos la dirección de la velocidad en dos puntos, el A y el O. Dado que el punto A sólo puede deslizar sobre el eje OX1, tenemos

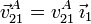
\vec{v}_{21}^A=v_{21}^A\,\vec{\imath}_1

Por otro lado, la velocidad en O debe ser tangente a la circunferencia del aro, pues éste sólo puede deslizar por el pasador. Como se indica en la figura adjunta, el punto de corte de las perpendiculares a las velocidades en esos dos puntos nos da la posición de I21.

2.2 Cálculo de vA21 y vC21

Para calcular analíticamente la posición del CIR necesitamos la velocidad angular y la velocidad en un punto. Al ser un movimiento plano sabemos que la velocidad angular es perpendicular al plano del movimiento

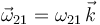
\vec{\omega}_{21}=\omega_{21}\,\vec{k}

siendo \vec{k} el vector unitario perpendicular al plano. Vamos a calcular la posición de los puntos A y C en el sistema "1", de modo que derivando los vectores de posición obtengamos las velocidades. A partir de ellas, usando la ecuación del campo de velocidades del movimiento {21} obtendremos el valor de ω21.

De la figura obtenemos

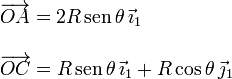
\begin{array}{l} \overrightarrow{OA} = 2R\,\mathrm{sen}\,\theta\,\vec{\imath}_1\\ \\ \overrightarrow{OC} = R\,\mathrm{sen}\,\theta\,\vec{\imath}_1 +R\cos\theta\,\vec{\jmath}_1 \end{array}

Estos vectores están expresados en el triedro "1", y son válidos en todo instante. Podemos entonces derivarlos para obtener las velocidades

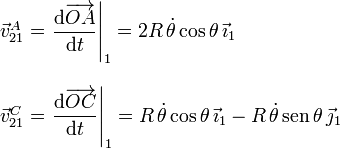
\begin{array}{l} \vec{v}_{21}^A=\left.\dfrac{\mathrm{d}\overrightarrow{OA}}{\mathrm{d}t}\right|_1=2R\,\dot{\theta}\cos\theta\,\vec{\imath}_1\\ \\ \vec{v}_{21}^C=\left.\dfrac{\mathrm{d}\overrightarrow{OC}}{\mathrm{d}t}\right|_1=R\,\dot{\theta}\cos\theta\,\vec{\imath}_1-R\,\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\jmath}_1 \end{array}

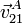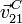
Usando la ecuación del campo de velocidades relacionamos \vec{v}_{21}^A y \vec{v}_{21}^C

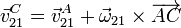
\vec{v}_{21}^C = \vec{v}_{21}^A+\vec{\omega}_{21}\times\overrightarrow{AC}

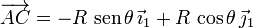Dado que \overrightarrow{AC}=-R\,\,\mathrm{sen}\,\theta\,\vec{\imath}_1+R\,\cos\theta\,\vec{\jmath}_1, haciendo el producto vectorial la ecuación vectorial se desdobla en dos ecuaciones escalares

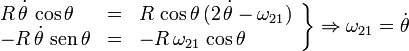
\left. \begin{array}{lcl} R\,\dot{\theta}\,\cos\theta&=&R\,\cos\theta\,(2\,\dot{\theta}-\omega_{21})\\ -R\,\dot{\theta}\,\,\mathrm{sen}\,\theta&=&-R\,\omega_{21}\,\cos\theta \end{array} \right\} \Rightarrow \omega_{21}=\dot{\theta}

Por tanto la reducción del movimiento {21} en el punto C es

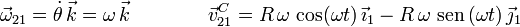
\vec{\omega}_{21}=\dot{\theta}\,\vec{k}=\omega\,\vec{k}\qquad\qquad\vec{v}_{21}^C = R\,\omega\,\cos(\omega t)\,\vec{\imath}_1-R\,\omega\,\,\mathrm{sen}\,(\omega t)\,\vec{\jmath}_1

Podemos calcular 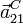\vec{a}_{21}^C derivando directamente en la velocidad calculada

\vec{a}_{21}^C=\left.\dfrac{\mathrm{d}\vec{v}_{21}^C}{\mathrm{d}t}\right|_1=-R\,\omega^2[\,\mathrm{sen}\,(\omega t)\,\vec{\imath}_1+\cos(\omega t)\,\vec{\jmath}_1]

Nos falta la determinación analítica de I21. Dada 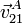\vec{v}_{21}^A, tenemos

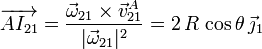
\overrightarrow{AI_{21}}=\dfrac{\vec{\omega}_{21}\times\vec{v}_{21}^A}{|\vec{\omega}_{21}|^2}=2\,R\,\cos{\theta}\,\vec{\jmath}_1

Podemos ver en la figura que este vector indica el mismo punto que la determinación gráfica.

2.3 Base y ruleta del movimiento {21}

2.3.1 Base

La base del movimiento {21} es el lugar geométrico descrito por el C.I.R. del movimiento, I21, visto desde el sólido "1". Este lugar geométrico es la curva descrita por I21 durante el movimiento del sólido "2". Para encontrarla, hemos de determinar la expresión del vector de posición de I21 visto desde el sólido "1", es decir, el vector 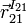\vec{r}^{I_{21}}_{21} . Como el origen de la escuadra del sólido "1" es el punto O, este vector es

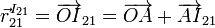
\vec{r}^{I_{21}}_{21} = \overrightarrow{OI}_{21} = \overrightarrow{OA} + \overrightarrow{AI}_{21}

De la geometría observamos que

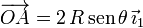
\overrightarrow{OA} = 2\,R\,\mathrm{sen}\,\theta\,\vec{\imath}_{1}

El otro vector lo hemos calculado en el apartado anterior. Entonces, el vector de posición de I21 visto desde el sólido "1" es

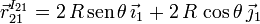
\vec{r}^{I_{21}}_{21} = 2\,R\,\mathrm{sen}\,\theta\,\vec{\imath}_{1} + 2\,R\,\cos\theta\,\vec{\jmath}_1

Esta curva está descrita en función del parámetro θ. Durante el movimiento, este ángulo va variando en el tiempo. Para encontrar la expresión de la curva que describe hemos de eliminar el parámetro. Tenemos

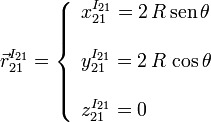
\vec{r}^{I_{21}}_{21} = \left\{ \begin{array}{l} x^{I_{21}}_{21} = 2\,R\,\mathrm{sen}\,\theta \\ \\ y^{I_{21}}_{21} = 2\,R\,\cos\theta \\ \\ z^{I_{21}}_{21} = 0 \end{array} \right.

Observando las expresiones de las componentes en X1 e Y1 vemos que

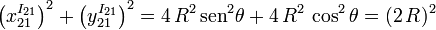
\left(x^{I_{21}}_{21}\right)^2 + \left(y^{I_{21}}_{21}\right)^2 = 4\,R^2\,\mathrm{sen}^2\theta + 4\,R^2\,\cos^2\theta = (2\,R)^2

Las ecuaciones implícitas de la base son

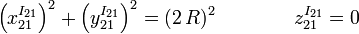
\left(x^{I_{21}}_{21}\right)^2 + \left(y^{I_{21}}_{21}\right)^2 = (2\,R)^2 \qquad\qquad z^{I_{21}}_{21} = 0

Esto es una circunferencia de radio 2R y centro en el punto O.

Obtenido de "http://tesla.us.es/wiki/index.php/Aro_con_deslizador_(G.I.A.)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace