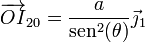6.3. Barra apoyada en placa
De Laplace
(Diferencias entre revisiones)
(→Centros instantáneos de rotación) |
(→Centros instantáneos de rotación) |
||
| Línea 9: | Línea 9: | ||
==Centros instantáneos de rotación== | ==Centros instantáneos de rotación== | ||
| + | |||
| + | [[Archivo:barra-placa-03.png|right]] | ||
| + | |||
;Del movimiento {01}: La placa realiza un movimiento de traslación horizontal, por lo que el centro instantáneo de rotación del movimiento {20} será un punto del infinito situado según la dirección vertical. | ;Del movimiento {01}: La placa realiza un movimiento de traslación horizontal, por lo que el centro instantáneo de rotación del movimiento {20} será un punto del infinito situado según la dirección vertical. | ||
| Línea 17: | Línea 20: | ||
:Queda por determinar la posición sobre este eje. Para ello necesitamos la dirección de la velocidad de algún punto en el movimiento {20} o el {02}. El más simple es el punto A, donde contactan la barra y la placa. Este contacto impone un vínculo sobre las posibles velocidades de A. En particular, impide que A, en el movimiento {02}, tenga una componente perpendicular a la propia barra, ya que de ser así atravesaría ésta. | :Queda por determinar la posición sobre este eje. Para ello necesitamos la dirección de la velocidad de algún punto en el movimiento {20} o el {02}. El más simple es el punto A, donde contactan la barra y la placa. Este contacto impone un vínculo sobre las posibles velocidades de A. En particular, impide que A, en el movimiento {02}, tenga una componente perpendicular a la propia barra, ya que de ser así atravesaría ésta. | ||
| - | Por tanto, <math>\vec{v}^A_{20}</math> es tangente a la propia barra. Ello implica que <math>I_{20}</math> se encuentra en la intersección de la perpendicular a la barra por A con el eje <math>OY_1</math>. | + | :Por tanto, <math>\vec{v}^A_{20}</math> es tangente a la propia barra. Ello implica que <math>I_{20}</math> se encuentra en la intersección de la perpendicular a la barra por A con el eje <math>OY_1</math>. |
| + | |||
| + | Podemos obtener las coordenadas de este punto empleando trigonometría. Si la altura de la placa es <math>a</math>, la distancia OA es la hipotenusa de un triángulo rectángulo, por lo que | ||
| + | |||
| + | <center><math>\left|\overrightarrow{OA}\right| = \frac{a}{\mathrm{sen}(\theta)}}</math></center> | ||
| + | |||
| + | La altura <math>h</math> es la hipotenusa de otro triángulo rectángulo, uno de cuyos catetos es OA. Por ello | ||
| + | |||
| + | <center><math>h = \frac{\left|\overrightarrow{OA}\right|}{\cos\left(\frac{\pi}{2}-\theta\right)} = \frac{a}{\mathrm{sen}^2(\theta)}</math></center> | ||
| + | |||
| + | En forma vectorial | ||
| + | |||
| + | <center><math>\overrightarrow{OI}_{20}=\frac{a}{\mathrm{sen}^2(\theta)}\vec{\jmath}_1</math></center> | ||
==Velocidades== | ==Velocidades== | ||
Revisión de 23:18 20 dic 2010
Contenido |
1 Enunciado
El esquema de la figura muestra una placa cuadrada de lado a (sólido ``0"), uno de cuyos lados desliza sobre el eje horizontal fijo OX1 (sólido “1”), mientras que la placa permanece contenida siempre en el plano vertical fijo OX1Y1. Sobre el vértice A de dicha placa se apoya en todo instante una varilla delgada (sólido “2”), que gira con velocidad angular constante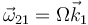 
, alrededor de su extremo articulado en el punto fijo O (ver figura). Se pide:
- Determinar gráficamente la posición de los centros instantáneos de rotación I21, I02 e I01.
- Calcular: i) La velocidad del vértice A de la placa en el movimiento de ésta respecto de los ejes fijos (movimiento {01}), expresada en función de la posición del sistema:
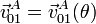. ii) La velocidad angular 
, correspondiente al movimiento relativo de la placa respecto de la varilla (movimiento {02}).
- Determinar analíticamente la posición del CIR del movimiento {02} (en función del ángulo θ).
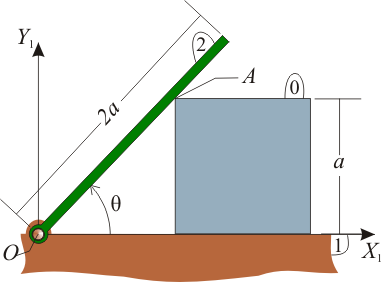
2 Centros instantáneos de rotación
- Del movimiento {01}
- La placa realiza un movimiento de traslación horizontal, por lo que el centro instantáneo de rotación del movimiento {20} será un punto del infinito situado según la dirección vertical.
- Del movimiento {21}
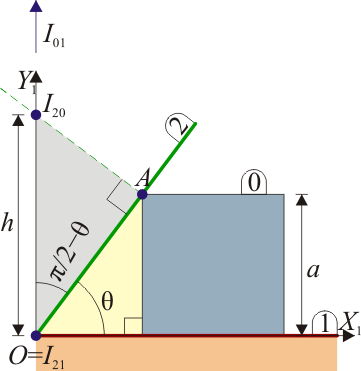
- La barra efectúa un movimiento de rotación en torno al punto en el cual se encuentra articulada. Este punto será el CIR I21, que de hecho en este caso se trata de un centro permanente y no solo instantáneo.
- Del movimiento {20}
- Por el teorema de los tres centros, el CIR I20 estará alineado con los otros dos. Puesto que I01 está en el infinito según la dirección vertical, el CIR I20 debe encontrarse en la vertical del punto O = I21, esto es, se trata de un punto del eje OY1.
- Queda por determinar la posición sobre este eje. Para ello necesitamos la dirección de la velocidad de algún punto en el movimiento {20} o el {02}. El más simple es el punto A, donde contactan la barra y la placa. Este contacto impone un vínculo sobre las posibles velocidades de A. En particular, impide que A, en el movimiento {02}, tenga una componente perpendicular a la propia barra, ya que de ser así atravesaría ésta.
- Por tanto,
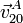es tangente a la propia barra. Ello implica que I20 se encuentra en la intersección de la perpendicular a la barra por A con el eje OY1.
Podemos obtener las coordenadas de este punto empleando trigonometría. Si la altura de la placa es a, la distancia OA es la hipotenusa de un triángulo rectángulo, por lo que
La altura h es la hipotenusa de otro triángulo rectángulo, uno de cuyos catetos es OA. Por ello
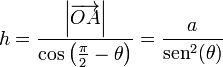
En forma vectorial
