Problemas de cinemática del sólido rígido (G.I.T.I.)
De Laplace
(→Ejemplo de movimiento de precesión) |
(→Ejemplo de campo de velocidades de un sólido) |
||
| Línea 1: | Línea 1: | ||
| + | ==[[Estudio de la velocidad de tres puntos]]== | ||
| + | En un hipotético sólido rígido, las posiciones y velocidades de tres puntos son respectivamente: | ||
| + | <center><math>\begin{array}{rclcrcl} | ||
| + | \overrightarrow{OA}&=&\vec{\imath}&\qquad & | ||
| + | \vec{v}^A & = & 4\vec{\imath}+2\vec{k}\\ | ||
| + | \overrightarrow{OB}&=&\vec{\jmath}&\qquad & | ||
| + | \vec{v}^B& = &2\vec{\imath}-2\vec{\jmath}-\vec{k}\\ | ||
| + | \overrightarrow{OC}&=&\vec{k}&\qquad & | ||
| + | \vec{v}^C&=&2\vec{\imath}-\vec{\jmath} | ||
| + | \end{array} | ||
| + | </math></center> | ||
| + | # Demuestre que estas velocidades son compatibles con la condición de rigidez. | ||
| + | # Halle la velocidad del punto <math>O(0,0,0)</math>. | ||
| + | # Calcule la velocidad del punto <math>\overrightarrow{OP}=2\vec{\imath}-2\vec{\jmath}-\vec{k}</math>. | ||
| + | # ¿Existe algún punto que tenga velocidad nula? ¿Dónde estaría situado? | ||
| + | Todas las cantidades están expresadas en las unidades del SI. | ||
| + | |||
==[[Ejemplo de campo de velocidades de un sólido]]== | ==[[Ejemplo de campo de velocidades de un sólido]]== | ||
Un campo de velocidades de un sistema de partículas tiene la expresión, en el SI, | Un campo de velocidades de un sistema de partículas tiene la expresión, en el SI, | ||
Revisión de 14:47 12 nov 2010
Contenido |
1 Estudio de la velocidad de tres puntos
En un hipotético sólido rígido, las posiciones y velocidades de tres puntos son respectivamente:
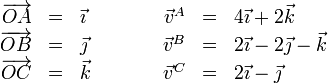
- Demuestre que estas velocidades son compatibles con la condición de rigidez.
- Halle la velocidad del punto O(0,0,0).
- Calcule la velocidad del punto
 .
.
- ¿Existe algún punto que tenga velocidad nula? ¿Dónde estaría situado?
Todas las cantidades están expresadas en las unidades del SI.
2 Ejemplo de campo de velocidades de un sólido
Un campo de velocidades de un sistema de partículas tiene la expresión, en el SI,
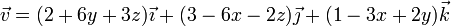
- Pruebe que corresponde al movimiento de un sólido rígido.
- Determine la velocidad angular y la velocidad de deslizamiento.
- Halle la ecuación del eje instantáneo de rotación y mínimo deslizamiento.
3 Velocidad de tres puntos de un sólido
Los vectores de posición y las velocidades de tres puntos de un sólido son, en el SI,
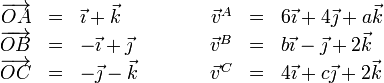
- Halle los valores de a, b, c.
- Halle la velocidad del punto
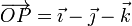 .
.
- Calcule la velocidad angular y la de deslizamiento
- Determine la posición del eje instantáneo de rotación y mínimo deslizamiento.
4 Ejemplo de diferentes estados de movimiento
Los vectores de posición y las velocidades de tres puntos de un sólido son, en el SI,
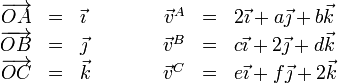
- ¿Qué restricciones impone la condición de rigidez a los valores de las incógnitas a, b, c, d, e y f?
- Halle los valores de estos parámetros si el sólido se encuentra en un estado de traslación instantáneo.
- Establezca la condición que deben cumplir las constantes si el estado de movimiento es una rotación pura.
5 Triángulo en movimiento helicoidal
El triángulo de vértices A, B y C, constituye un sólido rígido en movimiento respecto del sistema de referencia fijo OXYZ. De dicho movimiento se conocen los siguientes datos:
- Los vértices A y B permanecen en todo instante sobre el eje OZ, desplazándose ambos con igual velocidad instantánea:
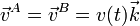 .
.
- El vértice C se mueve describiendo la hélice Γ, que en el sistema OXYZ está descrita por las ecuaciones paramétricas siguientes (donde R y h son constantes conocidas):

- Indique de forma razonada cuál es el eje instantáneo de rotación y mínimo deslizamiento en el movimiento descrito. Determine el vector velocidad angular en términos de los datos expresados en el enunciado.
- Exprese la componente normal de la aceleración del vértice C en un instante cualquiera, en función de los datos del enunciado.
- Para el caso en que v(t) = v0 (cte.), y h = R / 2, calcule la aceleración del vértice C. Determine la ley horaria s = s(t) con que el punto C describe su trayectoria.
6 Ejemplo de movimiento de precesión
El movimiento de precesión de una peonza puede describirse como una rotación en torno a un eje instantáneo que a su vez está rotando, manteniéndose fijo el punto de apoyo. Supongamos el caso particular
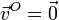
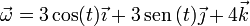
- Determine el campo de velocidades del sólido.
- Determine el campo de aceleraciones del sólido. ¿Es la aceleración de un punto igual a la derivada de la velocidad en ese punto respecto al tiempo?
- Halle, para cada instante las componentes intrínsecas de la aceleración y el radio de curvatura en el punto