Problemas de dinámica del punto material (G.I.T.I.)
De Laplace
(Diferencias entre revisiones)
(→Caída libre de un cuerpo) |
(→Caída libre de un cuerpo) |
||
| Línea 2: | Línea 2: | ||
Se trata de analizar el efecto de la fricción en la caída de un cuerpo pequeño, como puede ser una gota de lluvia. | Se trata de analizar el efecto de la fricción en la caída de un cuerpo pequeño, como puede ser una gota de lluvia. | ||
| - | <ol | + | <ol> |
| - | <li> Inicialmente consideramos despreciable el rozamiento. Si tenemos una gota de agua de radio 0.5 mm que cae verticalmente desde una altura ''h'' = 2 km | + | <li> Inicialmente consideramos despreciable el rozamiento. Si tenemos una gota de agua de radio 0.5 mm que cae verticalmente, partiendo del reposo desde una altura ''h'' = 2 km, ¿cuánto tiempo tarda en llegar al suelo? ¿Con qué velocidad impacta? Suponga g = 9.81 m/s².</li> |
<li> Para este mismo caso ideal, determine la energía cinética, potencial y mecánica en el punto inicial y el punto final del movimiento, así como para una altura <math>z</math> arbitraria.</li> | <li> Para este mismo caso ideal, determine la energía cinética, potencial y mecánica en el punto inicial y el punto final del movimiento, así como para una altura <math>z</math> arbitraria.</li> | ||
<li> Un cuerpo pequeño inmerso en un fluido experimenta una fuerza de fricción viscosa de la forma | <li> Un cuerpo pequeño inmerso en un fluido experimenta una fuerza de fricción viscosa de la forma | ||
| Línea 9: | Línea 9: | ||
<center><math>\vec{F}_r=-\gamma\vec{v}</math></center> | <center><math>\vec{F}_r=-\gamma\vec{v}</math></center> | ||
| - | siendo <math>\gamma</math> una constante de fricción que para una esfera en aire es de valor | + | ::siendo <math>\gamma</math> una constante de fricción que para una esfera en aire es de valor <math>\gamma = 3.4\times 10^{-4}\,\mathrm{kg}/(\mathrm{m}\cdot\mathrm{s})R</math> con <math>R</math> el radio de la partícula en m. Si se incluye esta fuerza, ¿qué ecuación de movimiento resulta para la velocidad vertical? </li> |
<li>Razone que, partiendo de la ecuación anterior, resulta que la velocidad tiende a un valor límite.</li> | <li>Razone que, partiendo de la ecuación anterior, resulta que la velocidad tiende a un valor límite.</li> | ||
| - | <li>Si prácticamente toda la caída de la gota se produce a la velocidad límite, ¿Con qué velocidad llega al suelo? ¿Cuánto | + | <li>Si prácticamente toda la caída de la gota se produce a la velocidad límite, ¿Con qué velocidad llega al suelo? ¿Cuánto tarda en caer? ¿Cuánta energía mecánica se pierde por el camino?</li> |
<li>Determine la expresión exacta de la velocidad y la altura como función del tiempo</li> | <li>Determine la expresión exacta de la velocidad y la altura como función del tiempo</li> | ||
</ol> | </ol> | ||
Revisión de 16:55 13 oct 2010
1 Caída libre de un cuerpo
Se trata de analizar el efecto de la fricción en la caída de un cuerpo pequeño, como puede ser una gota de lluvia.
- Inicialmente consideramos despreciable el rozamiento. Si tenemos una gota de agua de radio 0.5 mm que cae verticalmente, partiendo del reposo desde una altura h = 2 km, ¿cuánto tiempo tarda en llegar al suelo? ¿Con qué velocidad impacta? Suponga g = 9.81 m/s².
- Para este mismo caso ideal, determine la energía cinética, potencial y mecánica en el punto inicial y el punto final del movimiento, así como para una altura z arbitraria.
- Un cuerpo pequeño inmerso en un fluido experimenta una fuerza de fricción viscosa de la forma
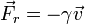
- siendo γ una constante de fricción que para una esfera en aire es de valor
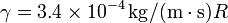con R el radio de la partícula en m. Si se incluye esta fuerza, ¿qué ecuación de movimiento resulta para la velocidad vertical?
- siendo γ una constante de fricción que para una esfera en aire es de valor
- Razone que, partiendo de la ecuación anterior, resulta que la velocidad tiende a un valor límite.
- Si prácticamente toda la caída de la gota se produce a la velocidad límite, ¿Con qué velocidad llega al suelo? ¿Cuánto tarda en caer? ¿Cuánta energía mecánica se pierde por el camino?
- Determine la expresión exacta de la velocidad y la altura como función del tiempo
2 Tensión de un péndulo
Empleando la ley de conservación de la energía, determine la velocidad con la que un péndulo de masa m y longitud l0 pasa por su punto más bajo, como función del ángulo máximo θ0 con el que se separa de la vertical.
Determine la tensión de la cuerda en el punto más bajo y el punto de máxima amplitud.
3 Caída a lo largo de una hélice
Una pequeña anilla de masa m esta obligada a moverse a lo largo de una hélice de radio A y paso de rosca b cuyo eje está situado verticalmente. La anilla se encuentra sometida a la acción de la gravedad y parte del reposo con velocidad nula. Cuando se encuentra a una altura z, ¿con qué velocidad se mueve? ¿Qué fuerza ejerce la anilla sobre la hélice?
