Problemas de dinámica del punto material (G.I.T.I.)
De Laplace
(Diferencias entre revisiones)
(→Caída libre de un cuerpo) |
(→Caída libre de un cuerpo) |
||
| Línea 2: | Línea 2: | ||
Se trata de analizar el efecto de la fricción en la caída de un cuerpo pequeño, como puede ser una gota de lluvia. | Se trata de analizar el efecto de la fricción en la caída de un cuerpo pequeño, como puede ser una gota de lluvia. | ||
| - | # Inicialmente consideramos despreciable el rozamiento. Si tenemos una gota de agua de radio 0.5 mm que cae verticalmente desde una altura ''h'' = 2 km, que | + | # Inicialmente consideramos despreciable el rozamiento. Si tenemos una gota de agua de radio 0.5 mm que cae verticalmente desde una altura ''h'' = 2 km, que parte del reposo, ¿cuánto tiempo tarda en llegar al suelo? ¿Con qué velocidad impacta? Suponga g = 9.81 m/s². |
# Para este mismo caso ideal, determine la energía cinética, potencial y mecánica en el punto inicial y el punto final del movimiento, así como para una altura <math>z</math> arbitraria. | # Para este mismo caso ideal, determine la energía cinética, potencial y mecánica en el punto inicial y el punto final del movimiento, así como para una altura <math>z</math> arbitraria. | ||
# Un cuerpo pequeño inmerso en un fluido experimenta una fuerza de fricción viscosa de la forma | # Un cuerpo pequeño inmerso en un fluido experimenta una fuerza de fricción viscosa de la forma | ||
Revisión de 15:47 13 oct 2010
Caída libre de un cuerpo
Se trata de analizar el efecto de la fricción en la caída de un cuerpo pequeño, como puede ser una gota de lluvia.
- Inicialmente consideramos despreciable el rozamiento. Si tenemos una gota de agua de radio 0.5 mm que cae verticalmente desde una altura h = 2 km, que parte del reposo, ¿cuánto tiempo tarda en llegar al suelo? ¿Con qué velocidad impacta? Suponga g = 9.81 m/s².
- Para este mismo caso ideal, determine la energía cinética, potencial y mecánica en el punto inicial y el punto final del movimiento, así como para una altura z arbitraria.
- Un cuerpo pequeño inmerso en un fluido experimenta una fuerza de fricción viscosa de la forma
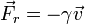
- siendo γ una constante de fricción que para una esfera en aire es de valor en el SI
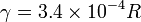con R el radio de la partícula en m. Si se incluye esta fuerza, ¿qué ecuación de movimiento resulta para la velocidad vertical?
- siendo γ una constante de fricción que para una esfera en aire es de valor en el SI
- Razone que, partiendo de la ecuación anterior, resulta que la velocidad tiende a un valor límite.
- Si prácticamente toda la caída de la gota se produce a la velocidad límite, ¿Con qué velocidad llega al suelo? ¿Cuánto atrda en caer? ¿Cuánta energía mecánica se pierde por el camino?
- Determine la expresión exacta de la velocidad y la altura como función del tiempo
