Corrientes atmosféricas
De Laplace
(Nueva página: ==Enunciado== La resistividad del aire en la atmósfera decrece exponencialmente con la altura como <center><math>\sigma^{-1}=r=r_1 \mathrm{e}^{-\alpha_1 z}+ r_2 \mathrm{e}^{-\alpha_...) |
(→Campo eléctrico en el aire) |
||
| Línea 29: | Línea 29: | ||
==Solución== | ==Solución== | ||
===Campo eléctrico en el aire=== | ===Campo eléctrico en el aire=== | ||
| + | Si el estado es estacionario se cumplirá que | ||
| + | |||
| + | <center><math>\nabla{\cdot}\mathbf{J}=0</math></center> | ||
| + | |||
| + | Si además consideramos que la dirección de la densidad de corriente es perpendicular al suelo (que es un conductor perfecto), nos queda <math>\mathbf{J}=J\mathbf{u}_{z}</math>, y la ecuación anterior se reduce a | ||
| + | |||
| + | <center><math>\frac{\partial{}J}{\partial{}z}=0</math>{{qquad}}<math>\Rightarrow</math>{{qquad}}<math>J=J_0=\mathrm{cte}</math></center> | ||
| + | |||
| + | La densidad de corriente es uniforme. A partir de este dato podemos obtener el campo en cualquier punto de la atmósfera | ||
| + | |||
| + | <center><math>E=\frac{J}{\sigma}=J_0r(z)=J_0\sum_ir_i\mathrm{e}^{-\alpha_iz}</math></center> | ||
| + | |||
| + | El valor de $J_0$ lo sacamos del valor del campo y de la resistividad en la superficie | ||
| + | |||
| + | <center><math>E_0=J_0\sum_ir_i\quad\Rightarrow\quad J_0=\frac{E_0}{r_1+r_2+r_3}= -1.33\times | ||
| + | 10^{-12} \frac{\mathrm{A}}{\mathrm{m}^2}</math></center> | ||
| + | |||
| + | El campo en función de la altura queda entonces | ||
| + | <center> | ||
| + | <math>E(z)=\sum_i E_i \mathrm{e}^{-\alpha_i z}\qquad E_i= | ||
| + | \frac{E_0r_i}{r_1+r_2+r_3} | ||
| + | </math></center> | ||
| + | Los valores de los coeficientes son | ||
| + | |||
| + | <center><math>E_1=-62.5\frac{\mathrm{V}}{\mathrm{m}}</math>{{qquad}} | ||
| + | <math>E_2=-29.6\frac{\mathrm{V}}{\mathrm{m}}</math>{{qquad}} | ||
| + | <math>E_3=-7.9\frac{\mathrm{V}}{\mathrm{m}}</math></center> | ||
| + | |||
| + | Según esto, la principal contribución al campo es la que decae más rápidamente. | ||
| + | |||
===Diferencia de potencial entre la superficie y la ionosfera=== | ===Diferencia de potencial entre la superficie y la ionosfera=== | ||
===Distribución de cargas=== | ===Distribución de cargas=== | ||
Revisión de 15:40 12 jun 2008
Contenido |
1 Enunciado
La resistividad del aire en la atmósfera decrece exponencialmente con la altura como
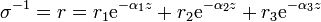
donde
El campo eléctrico en zonas despejadas de la superficie de la Tierra vale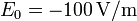 
. Este campo es prácticamente constante y va siempre en la dirección vertical.
A partir de estos datos halle
- El valor del campo eléctrico para un punto situado entre la superficie de la Tierra y la ionosfera (
).
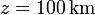- La diferencia de potencial entre la superficie y la ionosfera.
- La distribución de cargas en la atmósfera.
- La corriente total que llega a la superficie de la Tierra.
- La potencia necesaria para mantener esta corriente estacionaria
- Estime el tiempo que tardaría la atmósfera en descargarse si no existiera un mecanismo generador
2 Solución
2.1 Campo eléctrico en el aire
Si el estado es estacionario se cumplirá que
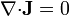
Si además consideramos que la dirección de la densidad de corriente es perpendicular al suelo (que es un conductor perfecto), nos queda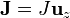 
, y la ecuación anterior se reduce a
J = J0 = cteLa densidad de corriente es uniforme. A partir de este dato podemos obtener el campo en cualquier punto de la atmósfera
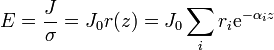
El valor de $J_0$ lo sacamos del valor del campo y de la resistividad en la superficie
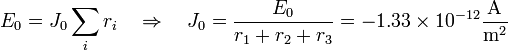
El campo en función de la altura queda entonces
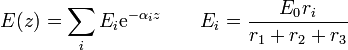
Los valores de los coeficientes son
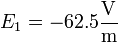
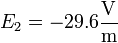
Según esto, la principal contribución al campo es la que decae más rápidamente.
