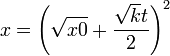2.4. Ejemplo de movimiento rectilíneo
De Laplace
(Diferencias entre revisiones)
(→Posición instantánea) |
(→Posición instantánea) |
||
| Línea 26: | Línea 26: | ||
La velocidad inicial la sacamos de que también en el instante inicial se cumple la relación del enunciado, por lo que | La velocidad inicial la sacamos de que también en el instante inicial se cumple la relación del enunciado, por lo que | ||
| - | <center><math>x = x_0 + \sqrt{kx_0} | + | <center><math>x = x_0 + t\sqrt{kx_0} + \frac{kt^2}{4}</math></center> |
Podemos escribir esta ecuación en la forma un poco más compacta | Podemos escribir esta ecuación en la forma un poco más compacta | ||
| - | <center><math>x = \left(\sqrt{x0 | + | <center><math>x = \left(\sqrt{x0}+\frac{\sqrt{k}t}{2}\right)^2</math></center> |
[[Categoría:Problemas de cinemática del punto material (G.I.T.I.)]] | [[Categoría:Problemas de cinemática del punto material (G.I.T.I.)]] | ||
Revisión de 15:56 3 oct 2010
1 Enunciado
Una partícula efectúa un movimiento rectilíneo tal que si x(t) es la posición a lo largo de la recta y v(t) la componente de la velocidad en dicha dirección, se cumple en todo instante
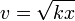
- Determine la aceleración en cada punto. ¿Qué tipo de movimiento efectúa la partícula?
- Si en t = 0 la partícula se encuentra en x = x0, ¿cuál es su posición en cualquier instante posterior?
2 Aceleración
La aceleración la obtenemos derivando la velocidad respecto al tiempo, lo cual se consigue aplicando la regla de la cadena,
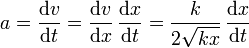
pero la derivada de la posición respecto al tiempo es la propia velocidad, por lo que

La aceleración es por tanto constante y el movimiento es uniformemente acelerado.
3 Posición instantánea
Al ser el movimiento rectilíneo uniformemente acelerado, la posición en cada instante es
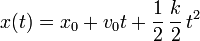
La velocidad inicial la sacamos de que también en el instante inicial se cumple la relación del enunciado, por lo que

Podemos escribir esta ecuación en la forma un poco más compacta