Esfera conductora rellena de dieléctrico con hueco
De Laplace
(Diferencias entre revisiones)
(→Sin carga eléctrica en el hueco) |
(→Sin carga eléctrica en el hueco) |
||
| Línea 7: | Línea 7: | ||
==Sin carga eléctrica en el hueco== | ==Sin carga eléctrica en el hueco== | ||
| - | [[Archivo:P1_sep_09_10_1.gif|left]]Analicemos primero el sistema antes de introducir los electrones en el hueco que hay en el centro del dieléctrico. Es decir, el sistema electrostático bajo estudio consiste en un conductor esférico de radio <math>2a</math> y espesor despreciable, relleno de una cáscara esférica de material dieléctrico ideal de permitividad dieléctrica <math>\varepsilon=5\varepsilon_0/2</math>, y radios interior y exterior <math>a</math> y <math>2a</math>, respectivamente. El conductor está conectado a una fuente de tensión constante de manera que la superficie conductora <math>Sigma_\mathrm{c}</math> va a ser una equipotencial de valor conocido <math>V_0</math>. | + | [[Archivo:P1_sep_09_10_1.gif|left]]Analicemos primero el sistema antes de introducir los electrones en el hueco que hay en el centro del dieléctrico. Es decir, el sistema electrostático bajo estudio consiste en un conductor esférico de radio <math>2a</math> y espesor despreciable, relleno de una cáscara esférica de material dieléctrico ideal de permitividad dieléctrica <math>\varepsilon=5\varepsilon_0/2</math>, y radios interior y exterior <math>a</math> y <math>2a</math>, respectivamente. El conductor está conectado a una fuente de tensión constante de manera que la superficie conductora <math>\Sigma_\mathrm{c}</math> va a ser una equipotencial de valor conocido <math>V_0</math>. |
==Con carga eléctrica en el hueco== | ==Con carga eléctrica en el hueco== | ||
[[Categoría:Problemas de materiales dieléctricos]] | [[Categoría:Problemas de materiales dieléctricos]] | ||
Revisión de 13:07 10 sep 2010
1 Enunciado
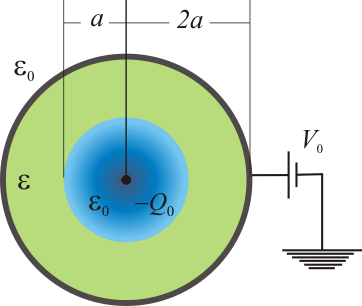
Una superficie esférica conductora ideal de pequeño espesor y radio 2a está rellena de un medio dieléctrico ideal homogéneo de permitividad , en cuyo centro hay un hueco de radio a. Estando la superficie conductora conectada a un potencial V0, el hueco es llenado con una nube de electrones cuya carga total es − Q0. Suponiendo que esta carga se distribuye uniformemente en el hueco y que en el medio dieléctrico no hay carga libre, resuelva las siguientes cuestiones:
, en cuyo centro hay un hueco de radio a. Estando la superficie conductora conectada a un potencial V0, el hueco es llenado con una nube de electrones cuya carga total es − Q0. Suponiendo que esta carga se distribuye uniformemente en el hueco y que en el medio dieléctrico no hay carga libre, resuelva las siguientes cuestiones:
- Determine los campos
 ,
,  y
y  , tanto en el interior como en el exterior de la esfera, antes y después de introducir la carga eléctrica en el hueco.
, tanto en el interior como en el exterior de la esfera, antes y después de introducir la carga eléctrica en el hueco.
- Halle la densidad de carga libre y la total en la interfaz r = a y en la cara interior y la exterior de la superficie conductora, antes y después de llenar el hueco.
- Calcule la energía electrostática almacenada en el sistema, antes y después de llenar el hueco.
2 Sin carga eléctrica en el hueco
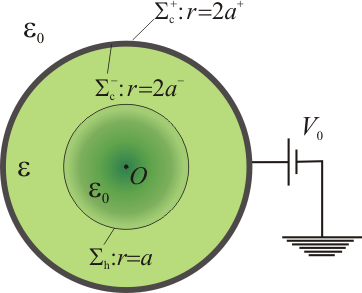
Analicemos primero el sistema antes de introducir los electrones en el hueco que hay en el centro del dieléctrico. Es decir, el sistema electrostático bajo estudio consiste en un conductor esférico de radio 2a y espesor despreciable, relleno de una cáscara esférica de material dieléctrico ideal de permitividad dieléctrica , y radios interior y exterior a y 2a, respectivamente. El conductor está conectado a una fuente de tensión constante de manera que la superficie conductora Σc va a ser una equipotencial de valor conocido V0.
, y radios interior y exterior a y 2a, respectivamente. El conductor está conectado a una fuente de tensión constante de manera que la superficie conductora Σc va a ser una equipotencial de valor conocido V0.