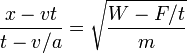1.3. Fórmulas dimensionalmente incorrectas

De Laplace

(Diferencias entre revisiones)

Revisión de 21:17 8 sep 2010

Contenido

1 Enunciado
2 Caso (a)
3 Caso (b)
4 Caso (c)
5 Caso (d)
6 Caso (e)
7 Caso (f)

1 Enunciado

Teniendo en cuenta las dimensiones calculadas en el problema anterior, indique cuáles de las siguientes expresiones son necesariamente incorrectas:

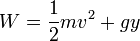
a) $W = \frac{1}{2}mv^2 + gy$

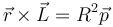
b) $\vec{r}\times\vec{L} = R^2\vec{p}$

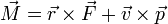
c) $\vec{M} = \vec{r}\times\vec{F}+\vec{v}\times\vec{p}$

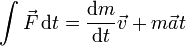
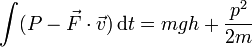
d) $\int \vec{F}\,\mathrm{d}t = \frac{\mathrm{d}m}{\mathrm{d}t}\vec{v}+ m\vec{a}t$

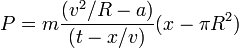
e) $\int (P-\vec{F}\cdot\vec{v})\,\mathrm{d}t = mgh + \frac{p^2}{2m}$

f) $P = m\frac{(v^2/R - a)}{(t-x/v)}(x-\pi R^2)$

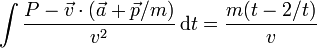
g) $\int\frac{P-\vec{v}\cdot(\vec{a}+\vec{p}/m)}{v^2}\,\mathrm{d}t = \frac{m(t-2/t)}{v}$

2 Caso (a)

Para que una fórmula sea dimensionalmente correcta los dos miembros de la ecuación deben tener las mismas dimensiones, y lo mismo debe ocurrir con cada uno de los sumandos de las sumas o diferencias que aparezcan en ella.

En el primer caso

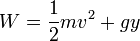
$W = \frac{1}{2}mv^2 + gy$

tenemos que el Trabajo trabajo tiene dimensiones de masa por velocidad al cuadrado

$[W]= M L^2T^{-2}\,$

De los términos del segundo miembro, el primero tiene claramente las mismas dimensiones que este

$\left[\frac{1}{2}mv^2\right] = [m][v]^2 = M(LT^{-1})^2 = ML^2T^{-2}\,$

mientras que el segundo tiene las dimensiones de una aceleración por una distancia

$[gy] = [a][y] = \left(LT^{-2}\right)L = L^2T^{-2}\,$

Puesto que aquí no hay ninguna potencia de la masa, que si aparece en los otros dos términos, esta fórmula es necesariamente incorrecta.

3 Caso (b)

En el segundo caso

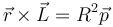
$\vec{r}\times\vec{L} = R^2\vec{p}$

el primer miembro tiene dimensiones de un momento cinético por una distancia

$\left[\vec{r}\times\vec{L}\right] = [r][L] = L(ML^2T^{-1}) = ML^3T^{-1}$

y el segundo de una cantidad de movimiento por una superficie

$\left[R^2\vec{p}\right] = L^2(MLT^{-1}) = ML^3T^{-1}$

Puesto que las dimensiones de los miembros son coincidentes, esta fórmula puede ser correcta. Lo que no quiere decir que lo sea.

4 Caso (c)

En el tercer caso

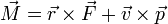
$\vec{M} = \vec{r}\times\vec{F}+\vec{v}\times\vec{p}$

El primer miembro es el momento de una fuerza, que tiene la misma ecuación dimensional que el trabajo

$[M]= M L^2 T^{-2}\,$

En el segundo miembro tenemos, para el primer término

$\left[\vec{r}\times\vec{F}\right] = [r][F]=L(MLT^{-2}) = M L^2T^{-2}$

y para el segundo

$\left[\vec{v}\times\vec{p}\right]= [v][p]= (LT^{-1})(MLT^{-1}) = ML^2T^{-2}$

Puesto que todos los términos tienen las mismas dimensiones, la fórmula puede ser correcta.

5 Caso (d)

En el caso

$\frac{x-vt}{t-v/a} = \sqrt{\frac{W-F/t}{m}}$

6 Caso (e)

7 Caso (f)

@@ Línea 72: / Línea 72: @@
 ==Caso (d)==
+En el caso
+<center><math>\frac{x-vt}{t-v/a} = \sqrt{\frac{W-F/t}{m}}</math></center>
 ==Caso (e)==
 ==Caso (f)==
 [[Categoría:Problemas de metrología]]

1.3. Fórmulas dimensionalmente incorrectas

De Laplace

Revisión de 21:17 8 sep 2010

Contenido

1 Enunciado

2 Caso (a)

3 Caso (b)

4 Caso (c)

5 Caso (d)

6 Caso (e)

7 Caso (f)

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES