Problemas de movimiento relativo (G.I.T.I.)
De Laplace
(→Rotación de un disco inclinado) |
|||
| Línea 1: | Línea 1: | ||
| + | ==[[Comparación de velocidades relativas de dos sólidos]]== | ||
Se tienen dos vagonetas A y B (sólidos “1” y “2”), que avanzan por raíles sobre el suelo horizontal (sólido “0”). En un momento dado las vagonetas se mueven paralelamente respecto al suelo con velocidades | Se tienen dos vagonetas A y B (sólidos “1” y “2”), que avanzan por raíles sobre el suelo horizontal (sólido “0”). En un momento dado las vagonetas se mueven paralelamente respecto al suelo con velocidades | ||
| Línea 54: | Línea 55: | ||
# Calcule la aceleración de los mismos puntos. | # Calcule la aceleración de los mismos puntos. | ||
| - | [[Categoría:Problemas de movimiento relativo de sólidos]] | + | [[Categoría:Problemas de movimiento relativo de sólidos|0]] |
Revisión de 13:34 15 ago 2010
1 Comparación de velocidades relativas de dos sólidos
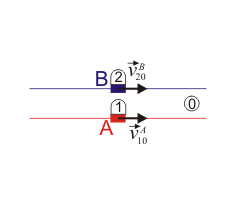
Se tienen dos vagonetas A y B (sólidos “1” y “2”), que avanzan por raíles sobre el suelo horizontal (sólido “0”). En un momento dado las vagonetas se mueven paralelamente respecto al suelo con velocidades
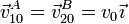
El vector de posición relativo entre las dos vagonetas es
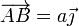
Los ejes de los tres sistemas se toman paralelos de forma que los vectores de las respectivas bases son coincidentes en ese instante.
Halle las velocidades relativas
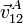y 
en los siguientes casos:
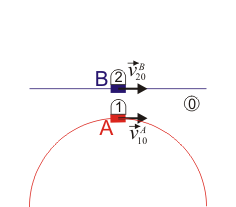
- Las vagonetas se mueven por vías rectilíneas paralelas.
- La vagoneta A se mueve por una vía circular de radio R, mientras que B se mueve por una vía rectilínea. El instante descrito es el de máximo acercamiento entre las dos vías.
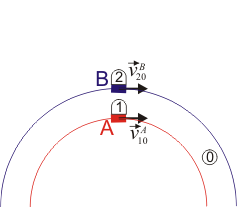
- Las dos se mueven por vías circulares concéntricas, de radios R y R + a, respectivamente.
- Las dos se mueven por arcos de circunferencia de radio R con centros en lados opuestos
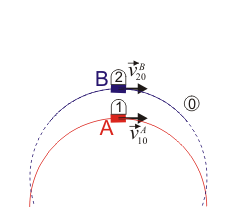
- Las dos se mueven por arcos de circunferencia de radio R con centros hacia el mismo lado
| 
| 
|
| (1) | (2) | (3) |
|---|---|---|
| 
| |
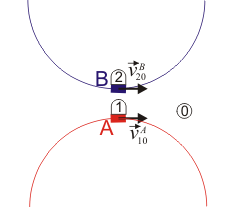
| (4) | (5) |
- Si además suponemos que los movimientos de las dos vagonetas son uniformes, calcule las aceleraciones relativas
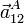y 
para los casos anteriores.
2 Rotación de un disco inclinado
Un disco de radio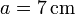 
en cuyo eje está ensartada una barra de longitud 
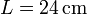se halla apoyada en el extremo de la barra y en el borde del disco. El disco rueda sobre una superficie horizontal, manteniendo fija la posición del extremo de la barra. El giro es uniforme, de forma que el centro del disco completa una revolución cada 
.
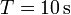Se consideran como sólido 1 la superficie horizontal, como sólido 0 la barra y como sólido 2 el disco. En un instante dado de toman los ejes del sistema 0 y 1 coincidentes y tales que OZ es la normal al plano horizontal que pasa por O, el extremo de la barra, OX es la recta horizontal que pasa por O y por A, el punto de contacto del disco con la mesa, y OY es la normal a los otros dos ejes.
- Determine la posición de los ejes instantáneos de rotación de los tres movimientos.
- Halle las velocidades de los puntos A (de contacto del disco con la mesa), B (diametralmente opuesto a A) y C (centro del disco), en los movimientos absoluto, relativo y de arrastre.
- Calcule la aceleración de los mismos puntos.
