Ejemplo de diferentes estados de movimiento
De Laplace
(Diferencias entre revisiones)
(→Condición de rigidez) |
(→Condición de rigidez) |
||
| Línea 45: | Línea 45: | ||
Podemos simplificar la notación haciendo | Podemos simplificar la notación haciendo | ||
| - | <center><math>a = 2+\gamma\qquad c = 2-\gamma</math>{{qquad}}{{qquad}} | + | <center><math>a = 2+\gamma\qquad c = 2-\gamma</math>{{qquad}}{{qquad}}<math>b = 2-\beta\qquad e = 2+\beta</math>{{qquad}}{{qquad}}<math>d = 2+\alpha\qquad f = 2-\alpha</math></center> |
| - | <math>b = 2-\beta\qquad e = 2+\beta</math>{{qquad}}{{qquad}} | + | |
| - | <math>d = 2+\alpha\qquad f = 2-\alpha</math></center> | + | |
[[Categoría:Problemas de cinemática del sólido rígido]] | [[Categoría:Problemas de cinemática del sólido rígido]] | ||
Revisión de 10:18 4 ago 2010
1 Enunciado
Los vectores de posición y las velocidades de tres puntos de un sólido son, en el SI,
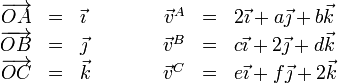
- ¿Qué restricciones impone la condición de rigidez a los valores de las incógnitas a, b, c, d, e y f?
- Halle los valores de estos parámetros si el sólido se encuentra en un estado de traslación instantáneo.
- Establezca la condición que deben cumplir las constantes si el estado de movimiento es una rotación pura.
2 Condición de rigidez
La condición cinemática de rigidez implica la equiproyectividad del campo de velocidades:
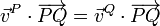
Aplicando esto a cada uno de los pares de puntos del enunciado tenemos, para los puntos A y B
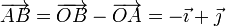
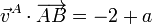
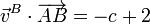

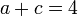
Repitiendo para A y C
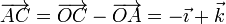
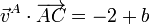
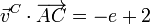

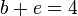
y para B y C
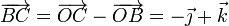
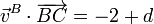
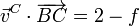

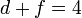
Los parámetros deben cumplir las condiciones
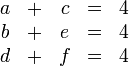
Podemos simplificar la notación haciendo








