Cuadrado y barra en equilibrio
De Laplace
(→Fuerzas vinculares) |
(→Fuerzas vinculares) |
||
| Línea 37: | Línea 37: | ||
pues no hay restricciones geométricas a rotaciones de la barra alrededor del extremo apoyado en ''A''. Es decir, el vínculo que establece “2” sobre “0” es equivalente a la fuerza <math>\mathbf{\Phi}_{02}</math> aplicada en el punto ''A''. | pues no hay restricciones geométricas a rotaciones de la barra alrededor del extremo apoyado en ''A''. Es decir, el vínculo que establece “2” sobre “0” es equivalente a la fuerza <math>\mathbf{\Phi}_{02}</math> aplicada en el punto ''A''. | ||
| - | Aplicando el teorema de las tres fuerzas al diagrama de sólido libre que hemos obtenido para la barra podemos asegurar que, para que ésta se halle en situación de equilibrio estático, es necesario que las rectas de acción de las tres fuerzas sean concurrentes en un punto. Observando dicho diagrama podemos establecer la relación que | + | Aplicando el teorema de las tres fuerzas al diagrama de sólido libre que hemos obtenido para la barra podemos asegurar que, para que ésta se halle en situación de equilibrio estático, es necesario que las rectas de acción de las tres fuerzas sean concurrentes en un punto. Observando dicho diagrama podemos establecer la relación que han de verificar las componentes de la fuerza vincular en ''A'': |
| - | <center><math>\frac{|\Phi_A^y|}{\Phi_A^x}=\frac{a}{a/2}=\mathrm{tan}\ \theta</math></center> | + | <center><math>\frac{|\Phi_A^y|}{\Phi_A^x}=\frac{a}{a/2}=2=\mathrm{tan}\ \theta</math></center> |
| + | |||
| + | siendo θ=''arc tan(2)'' el ángulo que forma <math>\mathbf{\Phi}_{02}</math> con la horizontal. En consecuencia, esta fuerza NO PUEDE SER COLINEAL CON LA BARRA. | ||
==Fuerzas y pares de enlace en el equilibrio== | ==Fuerzas y pares de enlace en el equilibrio== | ||
==Condiciones para deslizamiento y vuelco== | ==Condiciones para deslizamiento y vuelco== | ||
Revisión de 23:50 15 jul 2010
Contenido |
1 Enunciado
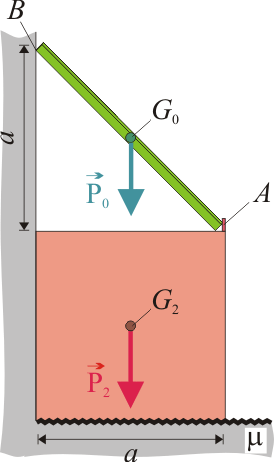
En el sistema de la figura, la barra de longitud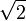 a y peso P0 se apoya en una pared vertical y en el vértice derecho superior de un cuadrado de lado a y peso P2. Ambos contactos son lisos. La base del cuadrado se apoya en el suelo con un contacto rugoso con coeficiente de rozamiento estático μ. En cada sólido, el peso se ejerce en su centro de masas.
a y peso P0 se apoya en una pared vertical y en el vértice derecho superior de un cuadrado de lado a y peso P2. Ambos contactos son lisos. La base del cuadrado se apoya en el suelo con un contacto rugoso con coeficiente de rozamiento estático μ. En cada sólido, el peso se ejerce en su centro de masas.
- Dibuja el diagrama de sólido libre de ambos sólidos.
- Calcula las fuerzas de reacción vincular y/o pares de enlace que actúan sobre cada sólido en la situación de equilibrio mecánico.
- Analiza las condiciones de equilibrio frente a deslizamiento y vuelco.
2 Diagrama de sólidos libres
El sistema está formado por un sólido fijo, consistente en el suelo y una pared vertical (sólido “1”), sobre el que se apoyan el cuadrado de lado a (sólido “2”), y la barra rígida de longitud 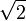 a (sólido “0”). El objetivo general de este ejercicio es el estudio del equilibrio mecánico del sistema cuando el cuadrado y la barra están contenidos en un plano vertical.
a (sólido “0”). El objetivo general de este ejercicio es el estudio del equilibrio mecánico del sistema cuando el cuadrado y la barra están contenidos en un plano vertical.
Comenzaremos dicho estudio aplicando los principios de fragmentación y de liberación para obtener los diagramas de sólidos libres para la barra y el cuadrado. Mediante esta operación, los vínculos geométricos derivados del contacto entre sólidos son sustituidos por unas fuerzas de reacción vincular (o pares de enlace) que contribuyen al equilibrio de forma idéntica a los vínculos. El diagrama de sólido libre se completa con las fuerzas no vinculares que actúan sobre el sólido. En este caso, dichas fuerzas serán los respectivos pesos de los sólidos “0” y “2”.
2.1 Diagrama del sólido “0”
2.1.1 Fuerzas no vinculares
La única fuerza no vincular que actúa sobre la barra o sólido “0” es la resultante de la acción de la gravedad sobre dicho sólido; es decir, su peso P0 aplicado en el centro de masas G0 que, asumiendo una distribución de masa homogénea, se encuentra en el centro geométrico del sólido. Esta fuerza se representa analíticamente mediante la siguiente reducción,

2.1.2 Fuerzas vinculares
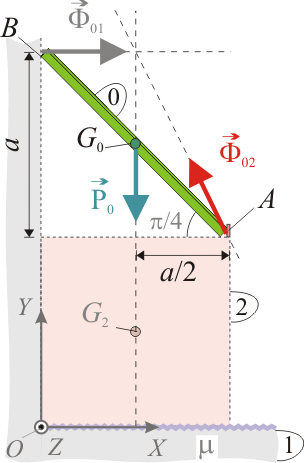
La barra apoya sus extremos A y B sobre el cuadrado “2” y la pared vertical “1”, respectivamente, mediante sendos contactos puntuales.
El contacto en B es liso y el vínculo o limitación que produce sobre la barra consiste en impedir que dicho extremo se mueva en el sentido negativo de la dirección OX. Es decir, se trata de un vínculo unilateral que no se opone a un posible movimiento del extremo B en cualquier dirección paralela al plano OYZ, ni tampoco en la dirección del eje OX si lo hace en el sentido positivo, ya que el contacto de la barra con la pared no impide que aquélla pueda llegar a despegarse. Además, como se trata de un contacto puntual, tampoco hay limitaciones a que la barra gire en torno a dicho extremo B. En consecuencia, la reacción vincular del sólido “1” sobre el “0” puede sustituirse por una fuerza que sólo actúa en sentido positivo de la dirección OX, y que está aplicada en el punto de contacto B, . Por tanto, el par de enlace que sustituye a este vínculo es,
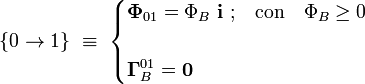
ya que el momento respecto de B de dicha fuerza vincular debe ser nulo.
El contacto del otro extremo de la barra en un punto cualquiera del lado horizontal superior del cuadrado también es un vínculo liso unilateral, que sólo impediría el desplazamiento de dicho extremo en el sentido negativo de la dirección OY. Por tanto, se sustituiría por una fuerza de reacción vincular que sólo contaría con una componente, siempre positiva, en la dirección de dicho eje. Obsérvese que esta fuerza vincular junto con el peso de la barra y la reacción {01} no podrían verificar la condición necesaria para el equilibrio de que la suma de todas las fuerzas aplicadas ha de ser nula.
Sin embargo, si en el vértice A del cuadrado se coloca un “tope” que impida el movimiento del extremo de la barra más allá de dicho punto, es posible que el sistema permanezca en equilibrio. En esta situación, el contacto puntual del sólido “0” con el vértice A del sólido “2” se sustituye por el par de enlace
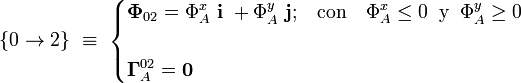
pues no hay restricciones geométricas a rotaciones de la barra alrededor del extremo apoyado en A. Es decir, el vínculo que establece “2” sobre “0” es equivalente a la fuerza 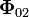 aplicada en el punto A.
aplicada en el punto A.
Aplicando el teorema de las tres fuerzas al diagrama de sólido libre que hemos obtenido para la barra podemos asegurar que, para que ésta se halle en situación de equilibrio estático, es necesario que las rectas de acción de las tres fuerzas sean concurrentes en un punto. Observando dicho diagrama podemos establecer la relación que han de verificar las componentes de la fuerza vincular en A:
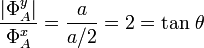
siendo θ=arc tan(2) el ángulo que forma 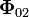 con la horizontal. En consecuencia, esta fuerza NO PUEDE SER COLINEAL CON LA BARRA.
con la horizontal. En consecuencia, esta fuerza NO PUEDE SER COLINEAL CON LA BARRA.