Cuadrado y barra en equilibrio

De Laplace

Contenido

1 Enunciado
2 Diagrama de sólidos libres
- 2.1 Diagrama del sólido “0”
  - 2.1.1 Fuerzas no vinculares
  - 2.1.2 Fuerzas vinculares
- 2.2 Diagrama del sólido “2”
  - 2.2.1 Fuerzas no vinculares
  - 2.2.2 Fuerzas vinculares
3 Fuerzas y pares de enlace en el equilibrio
- 3.1 Condiciones de equilibrio para el sólido “0”
- 3.2 Condiciones de equilibrio para el sólido “2”
4 Condiciones de equilibrio frente a deslizamiento y vuelco
- 4.1 Condición de no deslizamiento
- 4.2 Condición de no vuelco

1 Enunciado

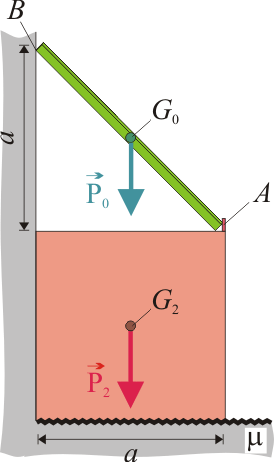
En el sistema de la figura, la barra de longitud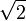 $\sqrt{2}$ a y peso P₀ se apoya en una pared vertical y en el vértice derecho superior de un cuadrado de lado a y peso P₂. Ambos contactos son lisos. La base del cuadrado se apoya en el suelo con un contacto rugoso con coeficiente de rozamiento estático μ. En cada sólido, el peso se ejerce en su centro de masas.

Dibuja el diagrama de sólido libre de ambos sólidos.
Calcula las fuerzas de reacción vincular y/o pares de enlace que actúan sobre cada sólido en la situación de equilibrio mecánico.
Analiza las condiciones de equilibrio frente a deslizamiento y vuelco.

2 Diagrama de sólidos libres

El sistema está formado por un sólido fijo, consistente en el suelo y una pared vertical (sólido “1”), sobre el que se apoyan el cuadrado de lado a (sólido “2”), y la barra rígida de longitud 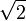$\sqrt{2}$ a (sólido “0”). El objetivo general de este ejercicio es el estudio del equilibrio mecánico del sistema cuando el cuadrado y la barra están contenidos en un plano vertical.

Comenzaremos dicho estudio aplicando los principios de fragmentación y de liberación para obtener los diagramas de sólidos libres para la barra y el cuadrado. Mediante esta operación, los vínculos geométricos derivados del contacto entre sólidos son sustituidos por unas fuerzas de reacción vincular (o pares de enlace) que contribuyen al equilibrio de forma idéntica a los vínculos. El diagrama de sólido libre se completa con las fuerzas no vinculares que actúan sobre el sólido. En este caso, dichas fuerzas serán los respectivos pesos de los sólidos “0” y “2”.

2.1 Diagrama del sólido “0”

2.1.1 Fuerzas no vinculares

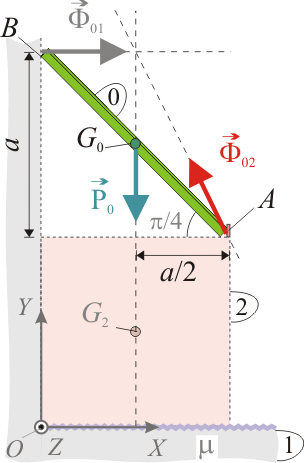
La única fuerza no vincular que actúa sobre la barra o sólido “0” es la resultante de la acción de la gravedad sobre dicho sólido; es decir, su peso P₀ aplicado en el centro de masas G₀ que, asumiendo una distribución de masa homogénea, se encuentra en el centro geométrico del sólido. Esta fuerza se representa analíticamente mediante la siguiente reducción,

$\left(\mathbf{P}_0;G_0\right)\ \equiv \ \bigg\{\mathbf{P}_0=-P_0\ \mathbf{j} \mathrm{;}\;\ \mathbf{M}_{G_0}(\mathbf{P}_0)=\mathbf{0}\bigg\}$

2.1.2 Fuerzas vinculares

La barra apoya sus extremos A y B sobre el cuadrado “2” y la pared vertical “1”, respectivamente, mediante sendos contactos puntuales.

El contacto en B es liso y el vínculo o limitación que produce sobre la barra consiste en impedir que dicho extremo se mueva en el sentido negativo de la dirección OX. Es decir, se trata de un vínculo unilateral que no se opone a un posible movimiento del extremo B en cualquier dirección paralela al plano OYZ, ni tampoco en la dirección del eje OX si lo hace en el sentido positivo, ya que el contacto de la barra con la pared no impide que aquélla pueda llegar a despegarse. Además, como se trata de un contacto puntual, tampoco hay limitaciones a que la barra gire en torno a dicho extremo B. En consecuencia, la reacción vincular del sólido “1” sobre el “0” puede sustituirse por una fuerza que sólo actúa en sentido positivo de la dirección OX, y que está aplicada en el punto de contacto B, . Por tanto, el par de enlace que sustituye a este vínculo es,

$\{0\leftarrow 1\}\ \equiv \ \begin{cases}\displaystyle \mathbf{\Phi}_{01}=\Phi_B\ \mathbf{i}\ \mathrm{;}\quad\mathrm{con}\quad \Phi_B\ge 0\\ \\ \displaystyle \mathbf{\Gamma}_B^{01}=\mathbf{0}\end{cases}$

ya que el momento respecto de B de dicha fuerza vincular debe ser nulo.

El contacto del otro extremo de la barra en un punto cualquiera del lado horizontal superior del cuadrado también es un vínculo liso unilateral, que sólo impediría el desplazamiento de dicho extremo en el sentido negativo de la dirección OY. Por tanto, se sustituiría por una fuerza de reacción vincular que sólo contaría con una componente, siempre positiva, en la dirección de dicho eje. Obsérvese que esta fuerza vincular junto con el peso de la barra y la reacción {01} no podrían verificar la condición necesaria para el equilibrio de que la suma de todas las fuerzas aplicadas ha de ser nula.

Sin embargo, si en el vértice A del cuadrado se coloca un “tope” que impida el movimiento del extremo de la barra más allá de dicho punto, es posible que el sistema permanezca en equilibrio. En esta situación, el contacto puntual del sólido “0” con el vértice A del sólido “2” se sustituye por el par de enlace

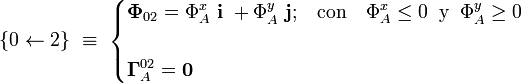
$\{0\leftarrow 2\}\ \equiv \ \begin{cases}\displaystyle \mathbf{\Phi}_{02}=\Phi_A^x\ \mathbf{i}\ + \Phi_A^y\ \mathbf{j}\mathrm{;}\quad\mathrm{con}\quad \Phi_A^x\le 0\;\; \mathrm{y}\;\; \Phi_A^y\ge 0\\ \\ \displaystyle \mathbf{\Gamma}_A^{02}=\mathbf{0}\end{cases}$

pues no hay restricciones geométricas a rotaciones de la barra alrededor del extremo apoyado en A. Es decir, el vínculo que establece “2” sobre “0” es equivalente a la fuerza 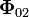$\mathbf{\Phi}_{02}$ aplicada en el punto A.

Aplicando el teorema de las tres fuerzas al diagrama de sólido libre que hemos obtenido para la barra podemos asegurar que, para que ésta se halle en situación de equilibrio estático, es necesario que las rectas de acción de las tres fuerzas sean concurrentes en un punto. Observando dicho diagrama podemos establecer la relación que han de verificar las componentes de la fuerza vincular en A:

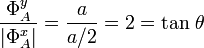
$\frac{\Phi_A^y}{|\Phi_A^x|}=\frac{a}{a/2}=2=\mathrm{tan}\ \theta$

siendo θ=arctan(2) el ángulo que forma 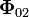$\mathbf{\Phi}_{02}$ con la horizontal. En consecuencia, esta fuerza NO PUEDE SER COLINEAL CON LA BARRA.

2.2 Diagrama del sólido “2”

2.2.1 Fuerzas no vinculares

Al igual que en el caso de la barra, la fuerza no vincular que actúa sobre el cuadrado es su peso P₂, aplicado en el centro de masas G₂, que también coincidirá con el punto donde se cortan todos los planos y/o ejes de simetría de la figura (centro geométrico). Se tendrá, por tanto,

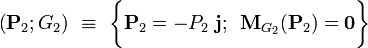
$\left(\mathbf{P}_2;G_2\right)\ \equiv \ \bigg\{\mathbf{P}_2=-P_2\ \mathbf{j} \mathrm{;}\;\ \mathbf{M}_{G_2}(\mathbf{P}_2)=\mathbf{0}\bigg\}$

2.2.2 Fuerzas vinculares

En el contacto entre dos sólidos “i” y “j”, y como consecuencia del principio de fragmentación, se tiene que el par de enlace correspondiente al vínculo ejercido por el sólido “i” sobre el “j”, es opuesto al del vínculo recíproco ejercido por “j” sobre “i”. Por tanto, la reacción vincular que ejerce la barra “0” sobre el cuadrado “2” estará caracterizada por el par de enlace,

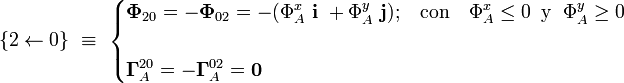
$\{2\leftarrow 0\}\ \equiv \ \begin{cases}\displaystyle \mathbf{\Phi}_{20}=-\mathbf{\Phi}_{02}=-(\Phi_A^x\ \mathbf{i}\ + \Phi_A^y\ \mathbf{j})\mathrm{;}\quad\mathrm{con}\quad \Phi_A^x\le 0\;\; \mathrm{y}\;\; \Phi_A^y\ge 0\\ \\ \displaystyle \mathbf{\Gamma}_A^{20}=-\mathbf{\Gamma}_A^{02}=\mathbf{0}\end{cases}$

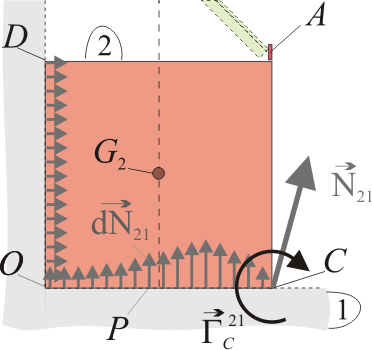
La reacción vincular del sólido fijo “1” sobre el cuadrado “2” está provocada por un contacto distribuido a lo largo de dos lados adyacentes del cuadrado: el lado vertical OD toca a la pared vertical del sólido “1”, mientras que el horizontal OC se apoya sobre el suelo. Además, el contacto en este segmento no es liso, estando caracterizado por un coeficiente de rozamiento estático de valor μ. 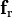Por tanto, la fuerza de reacción vincular $\mathbf{\Phi}_{21}$ correspondiente a este contacto podemos descomponerla en una parte lisa $\mathbf{N}_{21}$ que da cuenta de las restricciones geométricas y una $\mathbf{f}_\mathrm{r}$ que describe el rozamiento. 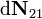La fuerza vincular lisa $\mathbf{N}_{21}$ va a ser la resultante de sendos sistemas de fuerzas paralelas infinitesimales $\mathrm{d}\mathbf{N}_{21}$ distribuidas a lo largo de los segmentos OD y OC. Estos sistemas impiden que, desde la posición de equilibrio, el cuadrado “2” se desplace en el sentido negativo de las direcciones OX y OY. Pero además, estos sistemas de fuerzas distribuidas van generar momentos vinculares no nulos respecto de determinados puntos; es decir, el contacto del cuadrado con el sólido fijo también va a impedir determinadas rotaciones del sólido “2” alrededor de ejes perpendiculares al plano del equilibrio.

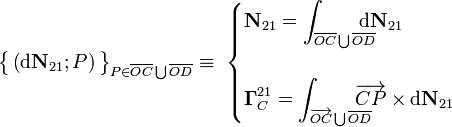
$\big\{\left(\mathrm{d}\mathbf{N}_{21};P\right)\big\}_{P\in\overline{OC}\bigcup\overline{OD}}\equiv \ \begin{cases}\displaystyle\mathbf{N}_{21}=\int_{\overline{OC}\bigcup\overline{OD}}\!\!\!\!\!\!\mathrm{d}\mathbf{N}_{21}\\ \\ \displaystyle \mathbf{\Gamma}_{C}^{21}=\int_{\overrightarrow{OC}\bigcup\overline{OD}}\!\!\!\!\!\!\overrightarrow{CP}\times\mathrm{d}\mathbf{N}_{21}\end{cases}$

El álgebra de vectores deslizantes nos permite llegar a la conclusión de que los dos sistemas aplicados conjuntamente son equivalentes a un único vector deslizante $\mathbf{N}_{21}$ aplicado en una recta de acción que no podemos determinar a priori. Sin embargo, podemos proceder a una desvinculación global del sólido “2” respecto del “1” mediante un par de enlace que describa las fuerzas que impiden los movimientos no compatibles con el vínculo: la resultante $\mathbf{N}_{21}$ deberá tener componentes positivas (o nulas) en las direcciones OX y OY, impidiendo sólo los desplazamiento antes indicados. Por otra parte, el vínculo no impedirá rotaciones alrededor de ejes paralelos a estos ejes, pero sí se opondrá a determinadas rotaciones en torno a direcciones paralelas al OZ. Por ejemplo, el contacto descrito con el sólido “1” impide completamente que el cuadrado gire alrededor de dicho eje. Pero si consideramos un eje paralelo a OZ que pase por el punto C, el vínculo permite rotaciones del cuadrado en sentido horario, pero no en el antihorario. Teniendo en cuenta que C es el punto donde podría romperse el equilibrio por vuelco del sólido “2”, reduciremos el par de enlace en este punto, incluyendo un momento vincular que sólo tiene componente negativa en la dirección OZ, para obstaculizar sólamente las rotaciones en sentido horario.

En cuanto a la fuerza de rozamiento 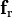$\mathbf{f}_\mathrm{r}$ , ésta sólo actúa en el contacto con el suelo. Según la ley de rozamiento seco de Coulomb, esta fuerza contribuye al equilibrio en la dirección tangente al contacto y con sentido opuesto al desplazamiento virtual del sólido. En consecuencia, 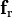$\mathbf{f}_\mathrm{r}$ tiene la dirección del eje OX y su sentido depende del posible sentido de desplazamiento del cuadrado: si el resto de fuerzas tienden a desplazarlo hacia la pared, de forma que N_x (componente “x” de $\mathbf{N}_{21}$ ) es positiva, la fuerza de rozamiento también será positiva (o nula); si las fuerzas restantes tiende a serparar el cuadrado de la pared, de manera que N_x es nula, la componente de la fuerza de rozamiento será negativa. Con todo esto, el sólido “2” puede ser liberado del vínculo ejercido por el fijo “1”, mediante la introducción del par de enlace,

$\{2\leftarrow 1\}\ \equiv \ \begin{cases}\displaystyle \mathbf{\Phi}_{21}=\mathbf{N}_{21}+\mathbf{f}_\mathrm{r}\\ \\ \displaystyle \mathbf{\Gamma}_C^{21}=\Gamma_C\mathbf{k}\mathrm{;}\quad\mathrm{con}\quad \Gamma_C\le 0\end{cases}$

donde las componentes de la resultante han de verificar las siguientes condiciones:

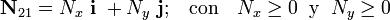
$\mathbf{N}_{21}=N_x\ \mathbf{i}\ + N_y\ \mathbf{j}\mathrm{;}\quad\mathrm{con}\quad N_x\ge 0\; \;\mathrm{y}\;\; N_y\ge 0$

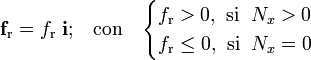
$\mathbf{f}_\mathrm{r}=f_\mathrm{r}\ \mathbf{i}\mathrm{;}\quad\mathrm{con}\quad\begin{cases} f_\mathrm{r}>0\mathrm{,}\;\;\mathrm{si}\; \; N_x>0\\ f_\mathrm{r}\le 0\mathrm{,}\;\;\mathrm{si}\; \; N_x=0\end{cases}$

Obsérvese que el contacto rugoso en la suelo también daría lugar a un par de rozamiento que no impediría pero sí se opondría a la libre rotación del sólido alrededor cualquier eje vertical. Sin embargo, podemos obviarlo ya que las fuerzas activas que intervienen en el sistema (pesos) generan momentos que no tienen componentes en esa dirección.

3 Fuerzas y pares de enlace en el equilibrio

Según el principio de fragmentación el sistema está en equilibrio cuando cada una de sus partes lo está; es decir, cada sólido liberado debe verificar las condiciones necesarias de que la resultante y el momento resultante de todas las fuerzas que actúan son ambos nulos. Esto nos permitirá calcular cuál es el valor de las fuerzas de reacción vincular y/o pares de enlace cuando el sistema bajo estudio se halla en equilibrio en la posición descrita.

3.1 Condiciones de equilibrio para el sólido “0”

Para que este sólido esté en equilibrio es necesario que la suma vectorial de su peso y de las dos fuerzas de reacción vincular sea nula:

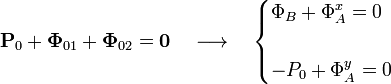
$\mathbf{P}_0+\mathbf{\Phi}_{01}+\mathbf{\Phi}_{02}=\mathbf{0}\quad\longrightarrow\quad\begin{cases}\displaystyle\Phi_B+\Phi_A^x=0\\ \\ \displaystyle -P_0+\Phi_A^y=0\end{cases}$

Tenemos un sistema de dos ecuaciones y tres incógnitas que podemos resolver completamente si añadimos las relación que obtuvimos para las componentes de la reacción vincular en A, mediante la aplicación del teorema de las tres fuerzas:

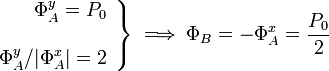
$\left.\begin{array}{r}\displaystyle \Phi_A^y=P_0\\ \\ \displaystyle \Phi_A^y/|\Phi_A^x|=2\end{array}\right\}\;\Longrightarrow\;\Phi_B=-\Phi_A^x=\frac{P_0}{2}$

Este mismo resultado lo podemos obtener a partir de la condición necesaria de momento resultante nulo:

$\mathbf{M}_A(\mathbf{P}_0)+\mathbf{\Gamma}_A^{01}+\mathbf{\Gamma}_A^{02}=\mathbf{0}$

Teniendo en cuenta cómo son las reducciones que describen las fuerzas que actúan sobre el sólido “0” liberado, la condición anterior nos lleva a la siguiente ecuación y resultado:

$\overrightarrow{AG}_0\times\mathbf{P}_0+\overrightarrow{AB}\times\mathbf{\Phi}_{01}=\frac{a}{2}\ P_0\ \mathbf{k}\ -\ a\Phi_B\ \mathbf{k}=\mathbf{0}\quad\Longrightarrow\quad\Phi_B=\frac{P_0}{2}=-\Phi_A^x$

En conclusión, las fuerzas de reacción vincular que actúa sobre los extremos A y B de la barra son, respectivamente,

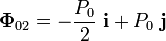
$\mathbf{\Phi}_{02}=-\frac{P_0}{2}\ \mathbf{i} +P_0\ \mathbf{j}\$ $\mathbf{\Phi}_{01}=\frac{P_0}{2}\ \mathbf{i}$

3.2 Condiciones de equilibrio para el sólido “2”

La fuerza de reacción vincular que ejerce el sólido “0” sobre el “2” es la opuesta a la acción recíproca; es decir,

$\mathbf{\Phi}_{20}=-\mathbf{\Phi}_{02}=\frac{P_0}{2}\ \mathbf{i} -P_0\ \mathbf{j}\$

Por otra parte, la suma de todas las fuerzas que actúan sobre el cuadrado liberado es...

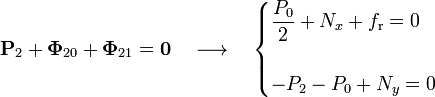
$\mathbf{P}_2+\mathbf{\Phi}_{20}+\mathbf{\Phi}_{21}=\mathbf{0}\quad\longrightarrow\quad\begin{cases}\displaystyle\frac{P_0}{2}+N_x+f_\mathrm{r}=0\\ \\ \displaystyle -P_2-P_0+N_y=0\end{cases}$

La segunda ecuación proporciona el valor de la componente vertical de la reacción reacción lisa $\mathbf{N}_{21}$ , mientras que la primera nos permite discutir el sentido y el valor de la fuerza de rozamiento. Analicemos cuál de las posibilidades consideradas en la definición de $\mathbf{\Phi}_{21}$ es compatible con la primera ecuación del sistema anterior. Obsérvese que dicha ecuación no se puede verificar si N_x y f_r son positivas, pero sí se cumple cuando N_x es nula y f_r negativa:

$N_y=P_2+P_0\ \mathrm{;}\qquad\qquad N_x+f_\mathrm{r}=-\frac{P_0}{2}\quad\Longleftrightarrow\quad\begin{cases}\displaystyle N_x=0\\ \\ \displaystyle f_\mathrm{r}=-\frac{P_0}{2}\end{cases}$

Por tanto, la resultante de la reacción vincular que el sólido fijo “1” ejerce sobre el cuadrado “2” cuando éste se halla en equilibrio es,

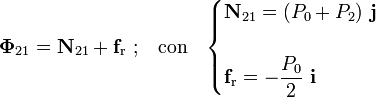
$\mathbf{\Phi}_{21}=\mathbf{N}_{21}+\mathbf{f}_\mathrm{r}\ \mathrm{;}\quad\mathrm{con}\quad\begin{cases}\displaystyle\mathbf{N}_{21}=(P_0+P_2)\ \mathbf{j}\\ \\ \displaystyle\mathbf{f}_\mathrm{r}=-\frac{P_0}{2}\ \mathbf{i}\end{cases}$

Pero el par de enlace correspondiente al vínculo 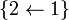$\{2\leftarrow 1\}$ tiene también un momento vincular, en general no nulo, que calcularemos exigiendo que en el equilibrio ha de cumplirse la condición necesaria

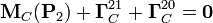
$\mathbf{M}_C(\mathbf{P}_2)+\mathbf{\Gamma}_C^{21}+\mathbf{\Gamma}_C^{20}=\mathbf{0}$

Teniendo en cuenta las expresiones de las reducciones que describen las fuerzas que actúan sobre el sólido “2” liberado, y cómo cambian éstas al cambiar los centros de reducción al punto C, se obtiene que, si el sistema está en equilibrio, se cumplirá

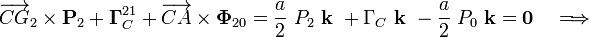
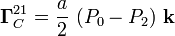
$\overrightarrow{CG}_2\times\mathbf{P}_2+\mathbf{\Gamma}_C^{21}+\overrightarrow{CA}\times\mathbf{\Phi}_{20}=\frac{a}{2}\ P_2\ \mathbf{k}\ +\Gamma_C\ \mathbf{k}\ -\frac{a}{2}\ P_0\ \mathbf{k}=\mathbf{0}\quad\Longrightarrow$ $\mathbf{\Gamma}_C^{21}=\frac{a}{2}\ (P_0-P_2)\ \mathbf{k}$

4 Condiciones de equilibrio frente a deslizamiento y vuelco

Con los resultados obtenidos en el apartado anterior, podemos asegurar que la barra permanecerá en equilibrio siempre que tenga sus extresmo apoyados en la pared y en el vértice A. Por tanto, el sistema dejará de estar en equilibrio cuando el cuadrado empiece a moverse, ya sea desplazándose paralelo al eje OX (deslizamiento), o girando alrededor de un eje perpendicular al plano de equilibrio y que pase por el vértice C (vuelco). 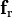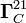Las causas de que el sistema deje de estar en equilibrio quedan perfectamente determinadas por las condiciones que deben verificar la fuerza de rozamiento $\mathbf{f}_\mathrm{r}$ y el momento vincular $\mathbf{\Gamma}_C^{21}$ .

4.1 Condición de no deslizamiento

Para que el cuadrado “2” no deslice sobre el plano horizontal del sólido fijo “1” es necesario que el módulo de la fuerza de rozamiento que modela el contacto rugoso sea menor o igual que el módulo de la componente normal de la fuerza de reacción vincular lisa, multiplicada por el coeficiente de rozamiento estático. Se obtiene así una relación entre dicho coeficientes y los pesos de los sólidos para que el sistema NO salga del equilibrio por deslizamiento del cuadrado:

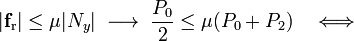
$|\mathbf{f}_\mathrm{r}|\le\mu|N_y|\;\longrightarrow\;\frac{P_0}{2}\le\mu(P_0+P_2)\quad\Longleftrightarrow$ $\mu\ge\frac{1}{2(1+P_2/P_0)}$

4.2 Condición de no vuelco

El cuadrado “2” no volcará sobre su vértice C siempre que su lado 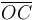$\overline{OC}$ permanezca apoyado sobre el suelo; es decir, siempre que el sistema de fuerzas vinculares paralelas distribuidos a lo largo de dicho lado, esté produciendo un momento respecto de C, que debe tener componente negativa en la dirección de OZ. Es decir, para que el sistema NO salga del equilibrio por vuelco del cuadrado, deberá cumplirse,

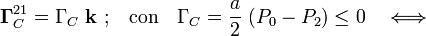
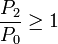
$\mathbf{\Gamma}_C^{21}=\Gamma_C\ \mathbf{k}\ \mathrm{;}\quad\mathrm{con}\quad\Gamma_C=\frac{a}{2}\ (P_0-P_2)\le 0\quad\Longleftrightarrow$ $\frac{P_2}{P_0}\ge 1$

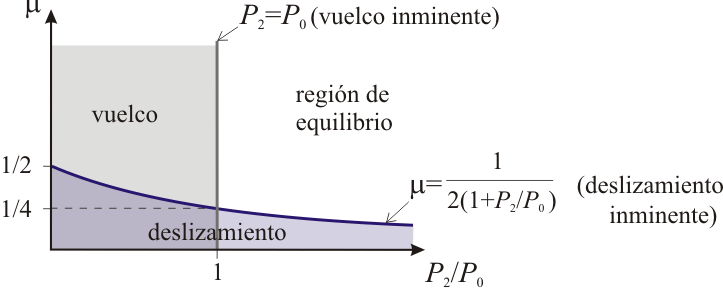
En el siguiente diagrama se distinguen las regiones de equilibrio frente a las de vuelco y deslizamiento, en función de los valores del coeficiente de rozamiento μ y de la relación P₂/P₀ entre los pesos de los dos sólidos:

Cuadrado y barra en equilibrio

De Laplace

Contenido

1 Enunciado

2 Diagrama de sólidos libres

2.1 Diagrama del sólido “0”

2.1.1 Fuerzas no vinculares

2.1.2 Fuerzas vinculares

2.2 Diagrama del sólido “2”

2.2.1 Fuerzas no vinculares

2.2.2 Fuerzas vinculares

3 Fuerzas y pares de enlace en el equilibrio

3.1 Condiciones de equilibrio para el sólido “0”

3.2 Condiciones de equilibrio para el sólido “2”

4 Condiciones de equilibrio frente a deslizamiento y vuelco

4.1 Condición de no deslizamiento

4.2 Condición de no vuelco

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES