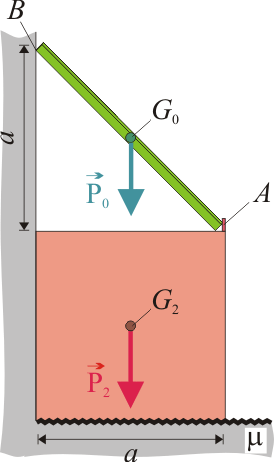
Cuadrado y barra en equilibrio
De Laplace
(Diferencias entre revisiones)
(→Diagrama de sólidos libres) |
(→Diagrama de sólidos libres) |
||
| Línea 7: | Línea 7: | ||
==Diagrama de sólidos libres== | ==Diagrama de sólidos libres== | ||
| - | El sistema formado por un sólido fijo (sólido “1”), consistente en el suelo y la pared vertical sobre la que se apoyan el cuadrado de lado ''a'' (sólido “2”), y la barra rígida de longitud <font size=-4><math>\sqrt{2}</math></font>''a''. | + | El sistema formado por un sólido fijo (sólido “1”), consistente en el suelo y la pared vertical sobre la que se apoyan el cuadrado de lado ''a'' (sólido “2”), y la barra rígida de longitud <font size=-4><math>\textstyle\sqrt{2}</math></font>''a''. |
==Fuerzas y pares de enlace en el equilibrio== | ==Fuerzas y pares de enlace en el equilibrio== | ||
==Condiciones para deslizamiento y vuelco== | ==Condiciones para deslizamiento y vuelco== | ||
Revisión de 18:48 15 jul 2010
Contenido |
1 Enunciado
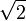a y peso P0 se apoya en una pared vertical y en el vértice derecho superior de un cuadrado de lado a y peso P2. Ambos contactos son lisos. La base del cuadrado se apoya en el suelo con un contacto rugoso con coeficiente de rozamiento estático μ. En cada sólido, el peso se ejerce en su centro de masas.
- Dibuja el diagrama de sólido libre de ambos sólidos.
- Calcula las fuerzas de reacción vincular y/o pares de enlace que actúan sobre cada sólido en la situación de equilibrio mecánico.
- Analiza las condiciones de equilibrio frente a deslizamiento y vuelco.
2 Diagrama de sólidos libres
El sistema formado por un sólido fijo (sólido “1”), consistente en el suelo y la pared vertical sobre la que se apoyan el cuadrado de lado a (sólido “2”), y la barra rígida de longitud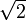 
a.
