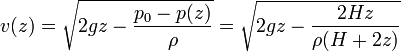Vaciado de un depósito cilíndrico
De Laplace
(→Velocidad de salida) |
(→Velocidad de salida) |
||
| Línea 41: | Línea 41: | ||
Por ello, podemos aproximar <math>v(z)</math> por cero y hallar la velocidad de salida como | Por ello, podemos aproximar <math>v(z)</math> por cero y hallar la velocidad de salida como | ||
| - | <center><math>v(z) = \sqrt{2 g z -\frac{p_0-p(z)}{\rho}} = \ | + | <center><math>v(z) = \sqrt{2 g z -\frac{p_0-p(z)}{\rho}} = \sqrt{2gz-\frac{2Hz}{\rho(H+2z)}}</math></center> |
==Vaciado parcial== | ==Vaciado parcial== | ||
==Valores numéricos== | ==Valores numéricos== | ||
Revisión de 21:23 12 jul 2010
Contenido |
1 Enunciado
Se tiene un recipiente cilíndrico de radio R y altura H abierto a la atmósfera, que se llena hasta una altura h = H / 2 de mercurio. Entonces, se cierra herméticamente por su parte superior, quedando una cámara de aire entre el mercurio y la tapa. En la parte inferior del recipiente se abre un pequeño orificio de radio a.
- Suponiendo que el aire dentro del recipiente se comporta como un gas ideal y que su temperatura permanece constante, encuentra la presión del aire cuando el mercurio llega hasta una altura z.
- Halla la expresión que da la velocidad con la que sale el mercurio cuando el nivel superior del mercurio está a una altura z
- ¿Puede vaciarse completamente el recipiente? Si no es así, encuentra la ecuación que da la altura final del mercurio en el recipiente.
- Supón que
, 
, 
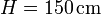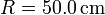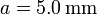y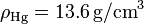 
. Calcula el valor numérico del apartado anterior y la cantidad de mercurio que ha salido del recipiente.
2 Presión del aire
Cuando el depósito se va vaciando, el tamaño de la cámara de aire va aumentando. Al aumentar el volumen, manteniéndose constante la temperatura, disminuye la presión, cumpliéndose la ley de Boyle
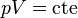
El volumen es inicialmente el de un cilindro de altura H / 2 y posteriormente H / 2 + z, por lo que la presión es
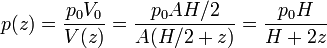
La diferencia de presiones entre el extremo inferior, abierto a la atmósfera, y el nivel superior es
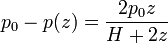
3 Velocidad de salida
Podemos calcular la velocidad de salida aplicando la ley de Bernouilli.
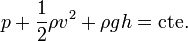
Igualando el valor de esta cantidad en 0 y en z, obtenemos
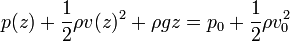
La velocidad con la que desciende el nivel del depósito es mucho menor que la que tiene el líquido que sale por el agujero, ya que por la ley de conservación de la masa
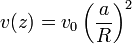
En concreto, para los datos de este problema, esta proporción es
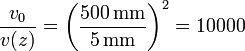
Por ello, podemos aproximar v(z) por cero y hallar la velocidad de salida como
