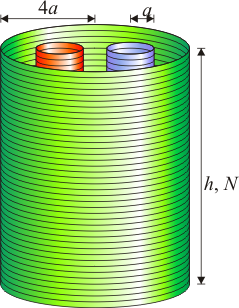
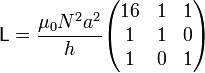Bobina con dos bobinas interiores
De Laplace
(→Coeficiente L22) |
(→Coeficiente L23) |
||
| Línea 66: | Línea 66: | ||
con lo que el coeficiente es | con lo que el coeficiente es | ||
| - | <center><math>L_{23}=L_{32}=0</math></center> | + | <center><math>L_{23}=L_{32}=0\,</math></center> |
===Matriz=== | ===Matriz=== | ||
Revisión de 12:28 29 jun 2010
Contenido |
1 Enunciado
Se tiene un sistema de tres solenoides formado por una bobina de radio 4a, gran longitud h y N vueltas. En el interior de esta bobina se encuentran, separadas, dos bobinas de radio a, misma longitud y mismo número de vueltas. Las ejes de las dos bobinas interiores se encuentran a una distancia 2a del de la grande. Las tres bobinas están arrolladas en el mismo sentido.
- Halle la matriz de coeficientes de autoinducción y de inducción mutua en este sistema. Desprecie los efectos de borde.
- Suponga que se conectan en serie las tres bobinas, de forma que por la bobina exterior circula una corriente + I y por las dos interiores una corriente − I. Exprese el campo magnético en todos los puntos del espacio para esta configuración
- Para el caso anterior, halle la energía magnética almacenada en el sistema. ¿Cuánto vale la autoinducción equivalente de la asociación?
2 Matriz de inducción
Un elemento de la matriz de coeficientes de autoinducción e inducción mutua, Lik se calcula como
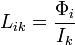
siendo Φi el flujo a través de la espira i cuando por la espira j circula una corriente Ij y por el resto no circula corriente alguna.
En este sistema tenemos tres boninas. Denominaremos “1” a la exterior y “2” y “3” a las interiores. Por la simetría de la matriz tenemos
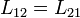
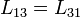
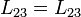
y por la simetría entres la bobinas 2 y 3 tenemos además
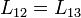
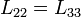
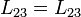
lo que nos deja con solo cuatro elementos diferentes

2.1 Coeficiente L11
El coeficiente L11 lo obtenemos suponiendo que por la bobina exterior circula una corriente I1 y por las demas no circula corriente. Esto quiere decir que las dos bobinas interiores no producen campo magnético alguno y pueden ser ignoradas para este cálculo.
Cuando se desprecian los efectos de borde y se supone que una bobina es de gran longitud, el campo magnético que produce es, aproximadamente,
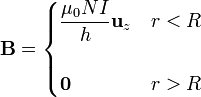
El flujo que atraviesa la bobina 1 será igual a N veces el flujo a través de cada una de las espiras que lo componen
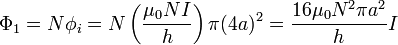
de donde el coeficiente es
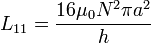
Este es un caso particular de la fórmula L = μN2S / h, que figura en la tabla.
2.2 Coeficiente L22
Usando el mismo razonamiento obtenemos los coeficientes L22 y L33, cambiando 4a por a:
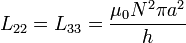
2.3 Coeficiente L12
Para hallar el coeficiente L21 (igual al L12 por la simetría de la matriz), necesitamos conocer el flujo a través de la bobina pequeña del campo debido a la bobina grande. Puesto que la bobina pequeña se encuentra completamente en el interior de la grande, el campo magnético de ésta la atraviesa completamente, resultando un flujo magnético
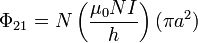
con lo que el coeficiente es
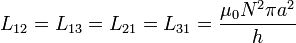
2.4 Coeficiente L23
Por último, para el coeficiente L32 necesitamos conocer el flujo a través de una de las bobina pequeñas del campo debido a la otra bobina pequeña. Puesto que la bobina pequeña se encuentra completamente en el exterior de la otra, el campo magnético de ésta no la atraviesa en absoluto (ya que el campo magnético producido por una bobina ideal es nulo fuera de ellas). Por tanto
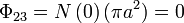
con lo que el coeficiente es
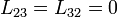
2.5 Matriz
Reuniendo todos los resultados tenemos la matriz de coeficientes de autoinducción y de inducción mutua