Cinemática de la partícula (G.I.T.I.)

De Laplace

(Diferencias entre revisiones)

Revisión de 19:23 18 jun 2010

1 Introducción

1.1 Cinemática

1.2 Partícula

1.3 Sistema de referencia

2 Trayectoria y ley horaria

2.1 Posición instantánea

Cuando una partícula se mueve por el espacio en cada instante ocupará una posición, que irá cambiando de forma continua con el tiempo (ya que la partícula no puede dematerializarse o teleportarse a otra posición).

En principio podemos etiquetar cada posición por una letra A, B, C,... Sin embargo, es más práctico identificar cada posición por su vector de posición cuyas componentes cartesianas son las distancias a los planos coordenados

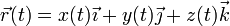
$\vec{r}(t) = x(t)\vec{\imath}+y(t)\vec{\jmath}+z(t)\vec{k}$

Aquí $x (t)$ , $y (t)$ y $z (t)$ son ciertas funciones continuas del tiempo.

Cuando se da la posición de la partícula como función del tiempo se dice que se conocen las ecuaciones horarias del movimiento.

2.2 Desplazamiento

El desplazamiento de una partícula en un intervalo $Δ t$ es la diferencia (vectorial) entre la posición al final del intervalo y la posición inicial

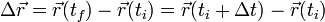
$\Delta \vec{r}= \vec{r}(t_f)-\vec{r}(t_i)=\vec{r}(t_i+\Delta t)-\vec{r}(t_i)$

Es importante hacer la distinción entre el desplazamiento y la distancia recorrida. Una partícula que recorra una curva cerrada tendrá un desplazamiento nulo, aunque la distancia recorrida no sea nula.

2.3 Desplazamiento diferencial

Cuando tenemos un desplazamiento entre dos instantes muy próximos,separados un intervalo $d t$ , se dice que tenemos un desplazamiento diferencial

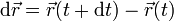
$\mathrm{d}\vec{r}=\vec{r}(t+\mathrm{d}t)-\vec{r}(t)$

Desde el punto de vista matemático, la palabra diferencial implica el proceso de tomar el límite 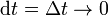$\mathrm{d}t = \Delta t\to 0$ , con lo que técnicamente un desplazamiento diferencial tiene longitud nula. Sin embargo, desde el punto de vista práctico, es más sencillo considerar un desplazamiento diferencial como de longitud muy pequeña comparada con las distancias típicas consideradas. Por ejemplo, si estamos hablando del desplazamiento de un vehículo sobre distancias de kilómetros a lo largo de minutos, un intervalo de milisegundos puede tratarse como un diferencial de tiempo, y un desplazamiento de milímetros puede considerarse un desplazamiento diferencial.

2.4 Trayectoria

Una partícula, al evolucionar en el tiempo, salvo cuando se encuentre en reposo, describe una curva en el espacio. Esta curva se conoce como la trayectoria de la partícula. Las ecuaciones horarias sirven como ecuaciones paramétricas de la trayectoria, siendo el tiempo el parámetro.

No obstante, a una misma trayectoria le pueden corresponder infinitas ecuaciones horarias, dependiendo del ritmo con el que se recorre la curva. Por ejemplo, las ecuaciones horarias

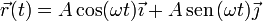
$\vec{r}(t) = A\cos(\omega t)\vec{\imath}+A\,\mathrm{sen}\,(\omega t)\vec{\jmath}$

y

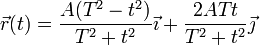
$\vec{r}(t) = \frac{A(T^2-t^2)}{T^2+t^2}\vec{\imath}+\frac{2ATt}{T^2+t^2}\vec{\jmath}$

corresponden a la misma trayectoria, una circunferencia horizontal.

En ocasiones, para indicar la trayectoria es preferible usar ecuaciones implícitas. En estas, se dan dos funciones (una sola, si el movimiento es plano), tales que

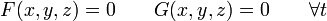
$F(x,y,z) = 0\qquad G(x,y,z) = 0\qquad \forall t$

Así, los dos ejemplos anteriores verifican

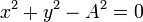
$x^2 + y^2 - A^2 = 0\,$ $z=0\,$

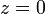
2.5 Parametrización de una trayectoria

La trayectoria que sigue una partícula es una propiedad puramente geométrica, independiente de si se recorre con una cierta velocidad u otra diferente. Por ello, para describir la trayectoria, considerada como curva en el espacio, no es preciso -ni siquiera conveniente- que en esta descripción aparezca explícitamente el tiempo. Todo lo que necesitamos es un método para identificar los puntos que componen la trayectoria.

Esto se consigue mediante una parametrización, que no es más que la asignación de etiquetas individuales para cada punto. Por conveniencia de cálculo, esta etiqueta consiste usualmente en una variable, que varía de forma continua a lo largo de la curva. Por ejemplo, para parametrizar una trayectoria circular, la variable más cómoda es el ángulo que forma el vector de posición con un eje fijo

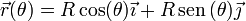
$\vec{r}(\theta)=R\cos(\theta)\vec{\imath}+R\,\mathrm{sen}\,(\theta)\vec{\jmath}$

y no es necesario interpretar $θ$ en términos de un tiempo (aunque puede hacerse, para visualizar la curva, al variar $θ$ progresivamente, recorremos la circunferencia con celeridad constante).

2.6 Parametrización natural

Para evitar el problema que supone identificar si las trayectorias de diferentes movimientos son coincidentes o no (debido a las diferencias en el ritmo con el que se recorre, o las variables empleadas para describir la trayectoria) se introduce la parametrización natural única para cada trayectoria (salvo un signo).

la idea es sencilla. En lugar de etiquetar cada punto de la trayectoria con el instante en que se pasa por él o con una variable arbitraria, se etiqueta usando la distancia $s$ a un punto de referencia:

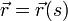
$\vec{r}=\vec{r}(s)$

Esto es exactamente lo que se hace en las carreteras, cuyos puntos se identifican mediante los postes kilométricos (y no por la hora en que un viajero concreto pase por cada punto).

La parametrización natural es única para cada trayectoria, salvo el signo correspondiente al sentido en que se recorre la curva (en el caso de la carretera, si desde Sevilla a Granada, o desde Granada a Sevilla). También el punto desde el que se empieza a contar queda libre.

A la variable $s$ , que mide la distancia sobre la curva se la denomina parámetro natural o parámetro arco. Para medir la distancia a lo largo de la curva lo que se hace es rectificar esta. Rectificar consiste en descomponer la curva en una infinitud de trozos de longitud diferencial, cada uno de los cuales se puede considerar aproximadamente rectilíneo, de forma que

$\mathrm{d}s=|\mathrm{d}\vec{r}|$

Sumando las longitudes de muchos trocitos diferenciales (esto es, integrando), obtenemos el valor del parámetro arco en un punto de la curva

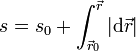
$s = s_0+\int_{\vec{r}_0}^\vec{r} |\mathrm{d}\vec{r}|$

3 Ley horaria

Cuando se tiene la trayectoria parametrizada en términos de la distancia medida sobre la curva la descripción se completa indicando cómo varía esta variable con el tiempo. Esta dependencia temporal se conoce como ley horaria:

$s = s(t)\,$

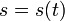
En el ejemplo de un coche que va de Sevilla a Granada, la ley horaria sería la hora a la que pasó por cada punto del camino sin prestar atención si en ese punto en concreto la carretera va hacia el sur o hacia el este.

Según esto, las ecuaciones horarias del movimiento pueden descomponerse en la trayectoria por un lado y la ley horaria por otro:

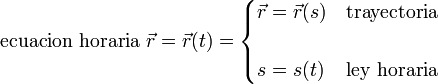
$\mbox{ecuacion horaria}\ \vec{r}=\vec{r}(t)=\begin{cases}\vec{r}=\vec{r}(s) & \mbox{trayectoria}\\ & \\ s=s(t)& \mbox{ley horaria}\end{cases}$

Si en lugar de un parámetro arco, se describe la trayectoria con otra variable, como el ángulo del ejemplo anterior, también se denomina ley horaria a la dependencia de esta variable con el tiempo. Así, en general:

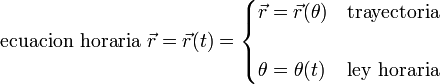
$\mbox{ecuacion horaria}\ \vec{r}=\vec{r}(t)=\begin{cases}\vec{r}=\vec{r}(\theta) & \mbox{trayectoria}\\ & \\ \theta=\theta(t)& \mbox{ley horaria}\end{cases}$

4 Velocidad

4.1 Velocidad media

Se define la velocidad media como el cociente entre el desplzamiento en un intervalo de tiempo y la duración de dicho intervalo

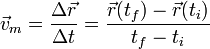
$\vec{v}_m = \frac{\Delta \vec{r}}{\Delta t} = \frac{\vec{r}(t_f)-\vec{r}(t_i)}{t_f-t_i}$

De la definición se desprende que

la velocidad es un vector: posee dirección y sentido, no solo un módulo (por tanto, decir que la velocidad es de 120 km/h es una información incompleta).
Posee unidades de distancia dividida por tiempo, que en el sistema internacional serán m/s.
La velocidad media depende del desplazamiento neto entre dos puntos, por tanto en un movimiento cíclico la velocidad media es nula, pues el punto final e inicial coinciden, independientemente de la distancia que se haya recorrido.
La velocidad no es igual a espacio partido por tiempo, sino a un desplazamiento dividido por un intervalo, esto es, lo que cuenta no es el valor absoluto de la distancia o la hora que marca el reloj, sino cuánto ha cambiado la posición y cuánto tiempo se ha empleado en realizar dicho desplazamiento.

4.2 Velocidad instantánea

El concepto de velocidad media no es especialmente útil, ya que solo nos informa del ritmo promedio, pero un movimiento concreto puede hacerse de forma irregular y normalmente interesa definir la velocidad en un momento dado, conocida como velocidad instantánea.

Consideremos un movimiento rectilíneo. Cuando decimos que en un instante dado la velocidad es de 120 km/h, ¿qué estamos diciendo exactamente? Evidentemente, no que durante la última hora se han recorrido 120 km, ya que igual sólo se llevan 10 minutos de marcha. Podríamos decir que durante el último minuto se han recorrido 2 km. ya que

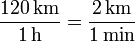
$\frac{120\,\mathrm{km}}{1\,\mathrm{h}} = \frac{2\,\mathrm{km}}{1\,\mathrm{min}}$

Esto ya es más preciso, pero aun no es del todo satisfactorio, ya que en un minuto hay tiempo suficiente a acelerar o frenar. Una mejor aproximación sería afirmar que en el último segundo se ha recorrido (1/30) km = 33.3 m. O podríamos decir que en la última décima de segundo se han recorrido 3.33 m,…

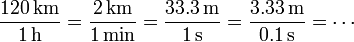
$\frac{120\,\mathrm{km}}{1\,\mathrm{h}} = \frac{2\,\mathrm{km}}{1\,\mathrm{min}}= \frac{33.3\,\mathrm{m}}{1\,\mathrm{s}}=\frac{3.33\,\mathrm{m}}{0.1\,\mathrm{s}}=\cdots$

En todos los casos la velocidad es de 120 km/h, pero cuanto más pequeño es el intervalo de tiempo considerado, más nos acercamos al ideal de medir la velocidad en un instante dado.

Definimos entonces la velocidad instantánea como el límite de la velocidad media cuando el intervalo de tiempo tiende a cero (se reduce a un instante)

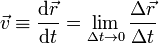
$\vec{v}\equiv\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\lim_{\Delta t\to 0}\frac{\Delta\vec{r}}{\Delta t}$

Matemáticamente, esto quiere decir que la velocidad instantánea es la derivada respecto al tiempo del vector de posición. En mecánica, una derivada respecto al tiempo suele representarse con un punto sobre la magnitud

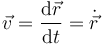
$\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t} = \dot{\vec{r}}$

De esta definición se deduce que:

La velocidad instantánea es un vector: posee módulo, dirección y sentido.
Las unidades de la velocidad instantánea son, en el SI m/s, aunque otras unidades como km/h son de uso frecuente.
La velocidad instantánea es un vector tangente a la trayectoria en cada punto.

4.3 Celeridad

4.3.1 Definición

En numerosas ocasiones no estamos interesados en la dirección y sentido de la velocidad, ya que sabiendo que es tangente a la trayectoria, podemos determinarlos geométricamente. En ese caso, la información necesaria se reduce al módulo de la velocidad. A esta cantidad se la conoce como celeridad:

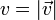
$v = \left|\vec{v}\right|$

Lo que en el habla cotidiana se denomina velocidad (“iba a 180 km/h”) es realmente una celeridad. Sin embargo, cuando la dirección y el sentido se dan por supuestos, la confusión entre los dos términos no es especialmente grave, pero siempre hay que tener en mente que la velocidad es realmente un vector, no un escalar.

Movimiento uniforme: La celeridad es la cantidad que nos informa del ritmo con el que recurre la trayectoria. En particular, cuando un movimiento se recorre a celeridad constante, se denomina movimiento uniforme.

Así, por ejemplo, un movimiento circular uniforme no es un movimiento a velocidad constante, ya que aunque su módulo no varíe, su dirección y sentido cambian a lo largo de la trayectoria.

4.3.2 Relación con la parametrización natural

La celeridad equivale a la velocidad con la que se recorre la distancia medida a lo largo de la curva

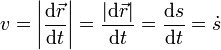
$v = \left|\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}\right| = \frac{|\mathrm{d}\vec{r}|}{\mathrm{d}t} = \frac{\mathrm{d}s}{\mathrm{d}t}=\dot{s}$

Esto quiere decir que, si conocemos la celeridad a lo largo de un movimiento, podemos determinar la distancia recorrida hasta un instante dado

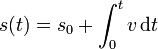
$s(t) = s_0 + \int_0^t v\,\mathrm{d}t$

Si podemos invertir esta relación y hallar el instante en que se llega a una distancia dada, $t = t (s)$ (lo que en contados casos es posible analíticamente), entonces podemos usar esta relación para escribir la curva mediante en su parametrización natural

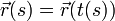
$\vec{r}(s) = \vec{r}(t(s))$

4.3.3 Ejemplo. Movimiento circular uniforme

Por ejemplo, supongamos el movimiento circular

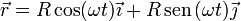
$\vec{r}=R\cos(\omega t)\vec{\imath} + R\,\mathrm{sen}\,(\omega t)\vec{\jmath}$

la celeridad la calculamos como el módulo de la velocidad

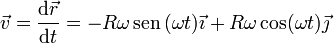
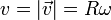
$\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}= -R\omega\,\mathrm{sen}\,(\omega t)\vec{\imath}+R\omega\cos(\omega t)\vec{\jmath}$ $\Rightarrow$ $v=|\vec{v}|=R\omega\,$

El parámetro arco es entonces, suponiendo que empezamos a medir desde $t = 0$

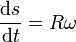
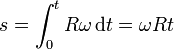
$\frac{\mathrm{d}s}{\mathrm{d}t}=R\omega$ $\Rightarrow$ $s =\int_0^t R\omega\,\mathrm{d}t = \omega R t$

Invirtiendo esta relación

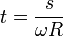
$t = \frac{s}{\omega R}$

lo que nos da la parametrización natural de la circunferencia

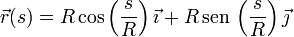
$\vec{r}(s)=R\cos\left(\frac{s}{R}\right)\vec{\imath}+R\,\mathrm{sen}\,\left(\frac{s}{R}\right)\vec{\jmath}$

5 Aceleración

Del mismo modo que se define la velocidad como la derivada de la posición respecto al tiempo, se define la aceleración instantánea como la derivada de la velocidad respecto al tiempo

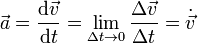
$\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=\lim_{\Delta t\to 0}\frac{\Delta\vec{v}}{\Delta t}=\dot{\vec{v}}$

Esto quiere decir que la aceleración es la segunda derivada del vector de posición respecto al tiempo, lo que se indica con dos puntos sobre la magnitud

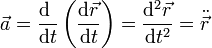
$\vec{a}=\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}\right)=\frac{\mathrm{d}^2\vec{r}}{\mathrm{d}t^2}=\ddot{\vec{r}}$

Un movimiento en el que la aceleración permanece constante en el tiempo se denomina uniformemente acelerado.

6 Componentes intrínsecas

6.1 Velocidad

De la definición de velocidad se deduce que se trata de un vector siempre tangente a la trayectoria, ya que un desplazamiento infinitesimal a lo largo de la trayectoria es un vector en la dirección de esta. Esto nos permite definir un vector unitario tangente a la trayectoria normalizando la velocidad

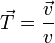
$\vec{T}=\frac{\vec{v}}{v}$

o, dicho de otra forma

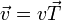
$\vec{v}=v\vec{T}$

La velocidad instantánea es un vector. La información sobre el módulo se recoge en la celeridad, mientras que la dirección y el sentido los da el vector unitario tangente a la trayectoria.

Puede demostrarse que el vector unitario tangente es independiente de la parametrización, esto es, que da igual que la trayectoria se recorra rápido o lento, el unitario tangente resultante es el mismo. Depende exclusivamente de la geometría de la trayectoria.

La única ambigüedad posible es el sentido. Dado que una misma curva puede recorrerse en un sentido o en el opuesto, existen dos posibles orientaciones para el vector tangente. Para un movimiento dado el unitario tangente siempre apunta en la dirección de avance de la partícula.

6.2 Aceleración

6.3 Triedro de Frenet

7 Ejemplos de movimientos

7.1 Rectilíneo

7.2 Parabólico

7.3 Circular

7.4 Helicoidal

7.5 Armónico simple

8 Problemas

@@ Línea 80: / Línea 80: @@
 ==Ley horaria==
-Cuando se tiene la trayectoria parametrizada en términos de una variable, que puede ser la distancia medida sobre la curva, pero también otra variable, como el ángulo del ejemplo anterior, la descripción se completa indicando cómo varía esta variable con el tiempo. Esta dependencia temporal se conoce como ''ley horaria'':
+Cuando se tiene la trayectoria parametrizada en términos de la distancia medida sobre la curva la descripción se completa indicando cómo varía esta variable con el tiempo. Esta dependencia temporal se conoce como ''ley horaria'':
 <center><math>s = s(t)\,</math></center>
@@ Línea 89: / Línea 89: @@
 <center><math>\mbox{ecuacion horaria}\ \vec{r}=\vec{r}(t)=\begin{cases}\vec{r}=\vec{r}(s) & \mbox{trayectoria}\\ & \\ s=s(t)& \mbox{ley horaria}\end{cases}</math></center>
+Si en lugar de un parámetro arco, se describe la trayectoria con otra variable, como el ángulo del ejemplo anterior, también se denomina ley horaria a la dependencia de esta variable con el tiempo. Así, en general:
+<center><math>\mbox{ecuacion horaria}\ \vec{r}=\vec{r}(t)=\begin{cases}\vec{r}=\vec{r}(\theta) & \mbox{trayectoria}\\ & \\ \theta=\theta(t)& \mbox{ley horaria}\end{cases}</math></center>
 ==Velocidad==