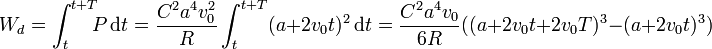Espira cuadrada en campo no uniforme
De Laplace
(→Fuerza magnética) |
|||
| (6 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| + | [[Archivo:espira-campo-x2.png|right]] | ||
| + | |||
En una región del espacio existe un campo magnético | En una región del espacio existe un campo magnético | ||
| Línea 15: | Línea 17: | ||
<center><math>I=\frac{\mathcal{E}}{R}=-\frac{1}{R}\,\frac{\mathrm{d}\Phi_m}{\mathrm{d}t}</math></center> | <center><math>I=\frac{\mathcal{E}}{R}=-\frac{1}{R}\,\frac{\mathrm{d}\Phi_m}{\mathrm{d}t}</math></center> | ||
| + | |||
| + | [[Archivo:espira-campo-x2-02.png|right]] | ||
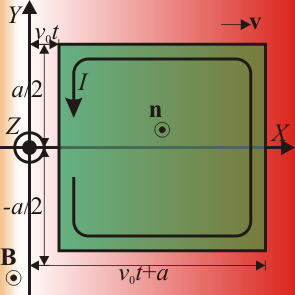
Calculamos el flujo magnético a través de un cuadrado apoyado en la espira. Asignamos un sentido de recorrido antihorario para la corriente, de forma que la normal a la superficie sobre la que calculamos el flujo va en la dirección de <math>\mathbf{u}_z</math>. | Calculamos el flujo magnético a través de un cuadrado apoyado en la espira. Asignamos un sentido de recorrido antihorario para la corriente, de forma que la normal a la superficie sobre la que calculamos el flujo va en la dirección de <math>\mathbf{u}_z</math>. | ||
| Línea 44: | Línea 48: | ||
Dividimos la espira en sus cuatro lados, numerándolos consecutivamente del 1 al 4. la fuerza sobre cada lado es | Dividimos la espira en sus cuatro lados, numerándolos consecutivamente del 1 al 4. la fuerza sobre cada lado es | ||
| + | |||
| + | [[Archivo:espira-campo-x2-03.png|right]] | ||
;Fuerza sobre el lado en <math>x=v_0t</math>: Para este lado la coordenada <math>x</math> vale lo mismo en todos los puntos (y su valor se puede sustituir en el integrando) mientras que la coordenada <math>y</math> varía desde <math>y = +a/2</math> a <math>y=-a/2</math> | ;Fuerza sobre el lado en <math>x=v_0t</math>: Para este lado la coordenada <math>x</math> vale lo mismo en todos los puntos (y su valor se puede sustituir en el integrando) mientras que la coordenada <math>y</math> varía desde <math>y = +a/2</math> a <math>y=-a/2</math> | ||
| Línea 61: | Línea 67: | ||
<center><math>\mathbf{F}_4 = I\int_{v_0t+a}^{v_0t} (\mathrm{d}x\,\mathbf{u}_x)\times(Cx^2\mathbf{u}_z)</math></center> | <center><math>\mathbf{F}_4 = I\int_{v_0t+a}^{v_0t} (\mathrm{d}x\,\mathbf{u}_x)\times(Cx^2\mathbf{u}_z)</math></center> | ||
| - | + | [[Archivo:espira-campo-x2-04.png|right]] | |
| - | con lo que la resultante queda | + | La fuerza sobre el lado inferior se cancela con la del superior, por ser integrales idénticas con los límites invertidos, con lo que la resultante queda |
<center><math>\mathbf{F}=\mathbf{F}_1+\mathbf{F}_3+\overbrace{\mathbf{F}_2+\mathbf{F}_4}^{=0}=ICa((v_0t+a)^2-(v_0t)^2)\mathbf{u}_x=ICa^2(a+2v_0t)\mathbf{u}_x</math></center> | <center><math>\mathbf{F}=\mathbf{F}_1+\mathbf{F}_3+\overbrace{\mathbf{F}_2+\mathbf{F}_4}^{=0}=ICa((v_0t+a)^2-(v_0t)^2)\mathbf{u}_x=ICa^2(a+2v_0t)\mathbf{u}_x</math></center> | ||
| Línea 72: | Línea 78: | ||
==Potencia y energía== | ==Potencia y energía== | ||
| + | La potencia disipada en la espira la obtenemos a partir de la ley de Joule: | ||
| + | |||
| + | <center><math>P=I^2R = \frac{C^2a^4(a+2v_0t)^2v_0^2}{R}</math></center> | ||
| + | |||
| + | Vemos que esta potencia disipada coincide con la desarrollada por la fuerza magnética | ||
| + | |||
| + | <center><math>|P_m| = |\mathbf{F}\cdot\mathbf{v}|=\frac{C^2a^4(a+2v_0t)^2v_0^2}{R}</math></center> | ||
| + | |||
| + | la energía disipada en un intervalo T es la integral de la potencia | ||
| + | |||
| + | <center><math>W_d = \int_t^{t+T}\!\!\! P\,\mathrm{d}t=\frac{C^2a^4v_0^2}{R}\int_t^{t+T}(a+2v_0t)^2\,\mathrm{d}t=\frac{C^2a^4v_0}{6R}((a+2v_0t+2v_0T)^3-(a+2v_0t)^3)</math></center> | ||
[[Categoría:Problemas de inducción electromagnética]] | [[Categoría:Problemas de inducción electromagnética]] | ||
última version al 21:22 13 jun 2010
Contenido |
1 Enunciado
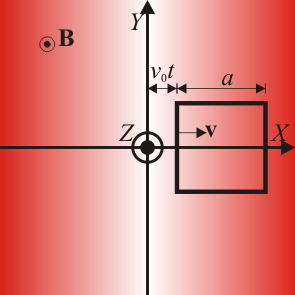
En una región del espacio existe un campo magnético

Una espira cuadrada de lado a y resistencia R se encuentra situada en el plano z = 0 con sus lados paralelos a los ejes. La espira se mueve de forma que su extremo trasero se encuentra en la posición x = v0t.
- Calcule la corriente que circula por la espira.
- Halle la fuerza que el campo magnético ejerce sobre la espira.
- Calcule la potencia disipada en la espira y la energía total disipada durante un tiempo T.
2 Corriente inducida
La corriente que circula por la espira se calcula por aplicación de la ley de Faraday
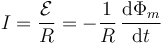
Calculamos el flujo magnético a través de un cuadrado apoyado en la espira. Asignamos un sentido de recorrido antihorario para la corriente, de forma que la normal a la superficie sobre la que calculamos el flujo va en la dirección de  .
.
El campo magnético en todos los puntos de esta superficie vale
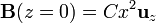
En este caso
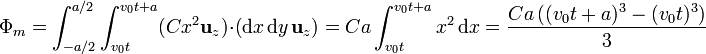
Derivando respecto al tiempo
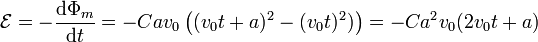
y finalmente la corriente es
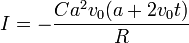
Esta corriente varía linealmente en el tiempo. Es nula en el instante t0 = − (a / 2) / v0, para el cual la espira está centrada en el campo. Es positiva para t < t0, en que el flujo magnético está disminuyendo y la corriente inducida tiende a aumentarlo. Es positiva para t > t0, en el que el flujo magnético está aumentando y la corriente intenta disminuirlo.
3 Fuerza magnética
La fuerza magnética la obtenemos de la expresión general

Aunque la corriente es la misma en toda la espira, esta fuerza no se anula por el ser el campo no uniforme, de forma parecida a lo que ocurre en el problema de la fuerza entre un hilo y una espira.
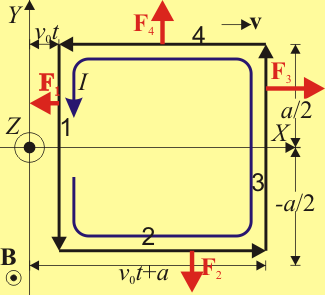
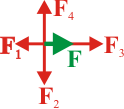
Dividimos la espira en sus cuatro lados, numerándolos consecutivamente del 1 al 4. la fuerza sobre cada lado es
- Fuerza sobre el lado en x = v0t
- Para este lado la coordenada x vale lo mismo en todos los puntos (y su valor se puede sustituir en el integrando) mientras que la coordenada y varía desde y = + a / 2 a y = − a / 2
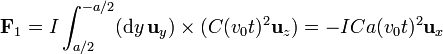
- Fuerza sobre el lado en y = − a / 2
- Para este lado varía la coordenada x desde x = v0t a x = v0t + a
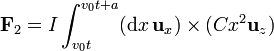
- Fuerza sobre el lado en x = v0t + a
- Para este lado de nuevo la coordenada x es constante y puede sustituirse mientras que la coordenada y varía ahora desde y = − a / 2 a y = + a / 2
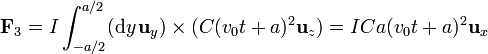
- Fuerza sobre el lado en y = + a / 2
- Para este lado varía la coordenada x desde x = v0t + a a x = v0t
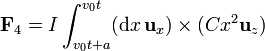
La fuerza sobre el lado inferior se cancela con la del superior, por ser integrales idénticas con los límites invertidos, con lo que la resultante queda
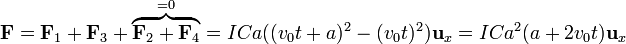
Sustituyendo el valor de la intensidad
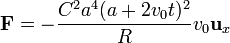
4 Potencia y energía
La potencia disipada en la espira la obtenemos a partir de la ley de Joule:
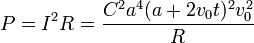
Vemos que esta potencia disipada coincide con la desarrollada por la fuerza magnética

la energía disipada en un intervalo T es la integral de la potencia