Entrar Página Discusión Historial Go to the site toolbox

Compresión adiabática irreversible

De Laplace

(Diferencias entre revisiones)
(Página creada con '==Enunciado== Se tiene un cilindro de paredes adiabáticas cerrado por un pistón móvil, también adiabático. En el interior del cilindro se encuentra un gas ideal sitiado ini…')
(→Caso numérico)
 
(18 ediciones intermedias no se muestran.)
Línea 1: Línea 1:
==Enunciado==
==Enunciado==
-
Se tiene un cilindro de paredes adiabáticas cerrado por un pistón móvil, también adiabático. En el interior del cilindro se encuentra un gas ideal sitiado inicialmente a una presión <math>p_0</math>, una temperatura <math>T_0</math> y ocupando un volumen <math>V_0</math>. De pronto se aumenta bruscamente la presión externa colocando una pesa sobre el pistón, de forma que la nueva presión externa pasa a ser <math>p_1>p_0</math>. El gas se comprime hasta que las presiones interna y externa vuelven a coincidir.
+
Se tiene un cilindro de paredes adiabáticas cerrado por un pistón móvil, también adiabático. En el interior del cilindro se encuentra un gas ideal sitiado inicialmente a una presión <math>p_0</math>, una temperatura <math>T_0</math> y ocupando un volumen <math>V_0</math>. De pronto se aumenta bruscamente la presión externa colocando una pesa sobre el pistón, de forma que la nueva presión externa pasa a ser <math>p_1=rp_0 >p_0</math>. El gas se comprime hasta que las presiones interna y externa vuelven a coincidir.
# Halle la temperatura final y el volumen final ocupado por el gas.
# Halle la temperatura final y el volumen final ocupado por el gas.
# Calcule el incremento de entropía del sistema
# Calcule el incremento de entropía del sistema
 +
# Supongamos que se trata de un gas diatómico a una presión inicial de 1&thinsp;atm, una temperatura inicial 20&deg;C y un volumen inicial de 100&thinsp;cm&sup3;. Si la presión final es de 2&thinsp;atm. ¿Cuál es el volumen y la temperatura finales, el trabajo realizado sobre el sistema y el aumento de entropía? Compárense estos resultados con lo que se obtienen en una compresión adiabática reversible desde 1 a 2&thinsp;atm.
==Temperatura y volumen final==
==Temperatura y volumen final==
 +
Al no tratarse de un proceso reversible, aunque se trata de un proceso adiabático no podemos usar la ecuación de Poisson <math>pV^\gamma=\mathrm{cte}</math>, sino que debemos ir a los conceptos básicos.
 +
 +
Tenemos que el proceso es adiabático, por lo que en él
 +
 +
<center><math>Q=0\,</math></center>
 +
 +
De acuerdo con el primer principio de la termodinámica, todo el trabajo realizado sobre el sistema se emplea en aumentar la energía interna
 +
 +
<center><math>W = \Delta U\,</math></center>
 +
 +
El trabajo lo podemos calcular sabiendo que la presión externa es constante en todo el proceso
 +
 +
<center><math>W = -\int_{V_0}^{V_1}p_1\,\mathrm{d}V = -p_1(V_1-V_0)</math></center>
 +
 +
El aumento de la energía interna lo podemos relacionar con el incremento de temperatura. Para un gas ideal
 +
 +
<center><math>\Delta U = nc_v(T_1-T_0) = \frac{c_v}{R}\left(nRT_1-nRT_0\right)=\frac{1}{\gamma-1}\left(p_1V_1-p_0V_0\right)</math></center>
 +
 +
Igualando el trabajo al aumento de la energía interna
 +
 +
<center><math>-p_1(V_1-V_0) = \frac{p_1V_1-p_0V_0}{\gamma-1}</math>{{tose}}<math>V_1 = \left(\frac{(\gamma-1)p_1+p_0}{p_1\gamma}\right)V_0=\left(\frac{(\gamma-1)r+1}{\gamma r}\right)V_0</math></center>
 +
 +
con <math>r = p_1/p_0</math>.
 +
 +
Una vez que tenemos el volumen final tenemos la temperatura
 +
 +
<center><math>T_1 = \frac{p_1V_1}{p_0V_0}T_0 = \left(\frac{(\gamma-1)r+1}{\gamma}\right)T_0</math></center>
 +
==Aumento de entropía==
==Aumento de entropía==
 +
El aumento de entropía lo calculamos a partir del conocimiento de la entropía de un gas ideal como función de la temperatura y la presión
 +
 +
<center><math>\Delta S = n c_p \ln\left(\frac{T_1}{T_0}\right)- nR \ln\left(\frac{p_1}{p_0}\right)= nc_p\ln\left(\frac{(1-\gamma)r+1}{\gamma}\right)-n R\ln(r) = \frac{p_0V_0}{T_0}\left(\frac{\gamma}{\gamma-1}\ln\left(\frac{(1-\gamma)r+1}{\gamma}\right)-\ln(r)\right)</math></center>
 +
 +
==Caso numérico==
 +
Tenemos que
 +
 +
<center><math>p_0 = 101325\,\mathrm{Pa}</math>{{qquad}}{{qquad}}<math>T_0=293\,\mathrm{K}</math>{{qquad}}{{qquad}}<math>V_0=10^{-4}\,\mathrm{m}^3</math>{{qquad}}{{qquad}}<math>p_1=2p_0\,</math>{{qquad}}{{qquad}}<math>\gamma = \frac{7}{5}</math></center>
 +
 +
Sustituyendo obtenemos
 +
 +
;Volumen: El volumen final es
 +
 +
<center><math>V_1 = \frac{9}{14}V_0 = 64.3\,\mathrm{cm}^3</math></center>
 +
 +
:En un proceso adiabático reversible, este volumen sería
 +
 +
<center><math>V'_1 = \left(\frac{p_0}{p_1}\right)^{1/\gamma}V_0 = 60.9\,\mathrm{cm}^3</math></center>
 +
 +
:esto es, la compresión es menor en el proceso adiabático irreversible.
 +
 +
;Temperatura: Sustituyendo igualmente obtenemos la temperatura final
 +
 +
<center><math>T_1 = \frac{9}{7}T_0 = 376\,\mathrm{K}</math></center>
 +
 +
:En un proceso adiabático reversible, la temperatura final sería
 +
 +
<center><math>T'_1 = \left(\frac{p_0}{p_1}\right)^{(\gamma-1)/\gamma}T_0 = 357\,\mathrm{K}</math></center>
 +
 +
:La temperatura aumenta más en el proceso irreversible que en el reversible.
 +
 +
;Trabajo y aumento de energía: En el proceso irreversible, el trabajo realizado sobre el sistema es
 +
 +
<center><math>W = \Delta U = -p_1(V_1-V_0)=\frac{p_0V_0(r-1)}{\gamma}=7.24\,\mathrm{J}</math></center>
 +
 +
:En un proceso reversible sería
 +
 +
<center><math>W' = \Delta U' = \frac{p_1V'_1-p_0V_0}{\gamma - 1} = 5.54\,\mathrm{J}</math></center>
 +
 +
;Entropía: La variación de entropía en el proceso reversible es
 +
 +
<center><math>\Delta S = 6.44\,\frac{\mathrm{mJ}}{\mathrm{K}}</math></center>
 +
 +
:En el proceso reversible alternativo, la variación de entropía es naturalmente nula.
 +
 +
[[Categoría: Problemas del segundo principio de la termodinámica]]

última version al 21:15 27 may 2010

Contenido

[ocultar]

1 Enunciado

Se tiene un cilindro de paredes adiabáticas cerrado por un pistón móvil, también adiabático. En el interior del cilindro se encuentra un gas ideal sitiado inicialmente a una presión p0, una temperatura T0 y ocupando un volumen V0. De pronto se aumenta bruscamente la presión externa colocando una pesa sobre el pistón, de forma que la nueva presión externa pasa a ser p1 = rp0 > p0. El gas se comprime hasta que las presiones interna y externa vuelven a coincidir.

  1. Halle la temperatura final y el volumen final ocupado por el gas.
  2. Calcule el incremento de entropía del sistema
  3. Supongamos que se trata de un gas diatómico a una presión inicial de 1 atm, una temperatura inicial 20°C y un volumen inicial de 100 cm³. Si la presión final es de 2 atm. ¿Cuál es el volumen y la temperatura finales, el trabajo realizado sobre el sistema y el aumento de entropía? Compárense estos resultados con lo que se obtienen en una compresión adiabática reversible desde 1 a 2 atm.

2 Temperatura y volumen final

Al no tratarse de un proceso reversible, aunque se trata de un proceso adiabático no podemos usar la ecuación de Poisson pVγ = cte, sino que debemos ir a los conceptos básicos.

Tenemos que el proceso es adiabático, por lo que en él

Q=0\,

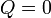
De acuerdo con el primer principio de la termodinámica, todo el trabajo realizado sobre el sistema se emplea en aumentar la energía interna

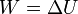
W = \Delta U\,

El trabajo lo podemos calcular sabiendo que la presión externa es constante en todo el proceso

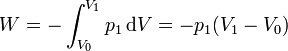
W = -\int_{V_0}^{V_1}p_1\,\mathrm{d}V = -p_1(V_1-V_0)

El aumento de la energía interna lo podemos relacionar con el incremento de temperatura. Para un gas ideal

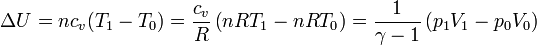
\Delta U = nc_v(T_1-T_0) = \frac{c_v}{R}\left(nRT_1-nRT_0\right)=\frac{1}{\gamma-1}\left(p_1V_1-p_0V_0\right)

Igualando el trabajo al aumento de la energía interna

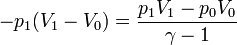
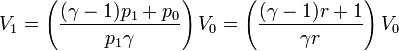
-p_1(V_1-V_0) = \frac{p_1V_1-p_0V_0}{\gamma-1}   \Rightarrow   V_1 = \left(\frac{(\gamma-1)p_1+p_0}{p_1\gamma}\right)V_0=\left(\frac{(\gamma-1)r+1}{\gamma r}\right)V_0

con r = p1 / p0.

Una vez que tenemos el volumen final tenemos la temperatura

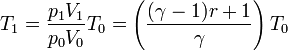
T_1 = \frac{p_1V_1}{p_0V_0}T_0 = \left(\frac{(\gamma-1)r+1}{\gamma}\right)T_0

3 Aumento de entropía

El aumento de entropía lo calculamos a partir del conocimiento de la entropía de un gas ideal como función de la temperatura y la presión

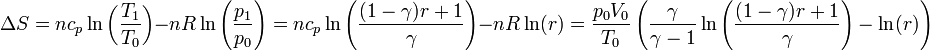
\Delta S = n c_p \ln\left(\frac{T_1}{T_0}\right)- nR \ln\left(\frac{p_1}{p_0}\right)= nc_p\ln\left(\frac{(1-\gamma)r+1}{\gamma}\right)-n R\ln(r) = \frac{p_0V_0}{T_0}\left(\frac{\gamma}{\gamma-1}\ln\left(\frac{(1-\gamma)r+1}{\gamma}\right)-\ln(r)\right)

4 Caso numérico

Tenemos que

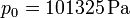
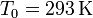
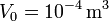
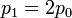
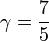
p_0 = 101325\,\mathrm{Pa}        T_0=293\,\mathrm{K}        V_0=10^{-4}\,\mathrm{m}^3        p_1=2p_0\,        \gamma = \frac{7}{5}

Sustituyendo obtenemos

Volumen
El volumen final es
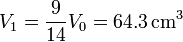
V_1 = \frac{9}{14}V_0 = 64.3\,\mathrm{cm}^3
En un proceso adiabático reversible, este volumen sería
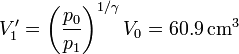
V'_1 = \left(\frac{p_0}{p_1}\right)^{1/\gamma}V_0 = 60.9\,\mathrm{cm}^3
esto es, la compresión es menor en el proceso adiabático irreversible.
Temperatura
Sustituyendo igualmente obtenemos la temperatura final
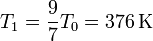
T_1 = \frac{9}{7}T_0 = 376\,\mathrm{K}
En un proceso adiabático reversible, la temperatura final sería
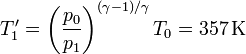
T'_1 = \left(\frac{p_0}{p_1}\right)^{(\gamma-1)/\gamma}T_0 = 357\,\mathrm{K}
La temperatura aumenta más en el proceso irreversible que en el reversible.
Trabajo y aumento de energía
En el proceso irreversible, el trabajo realizado sobre el sistema es
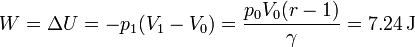
W = \Delta U = -p_1(V_1-V_0)=\frac{p_0V_0(r-1)}{\gamma}=7.24\,\mathrm{J}
En un proceso reversible sería
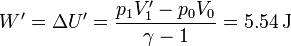
W' = \Delta U' = \frac{p_1V'_1-p_0V_0}{\gamma - 1} = 5.54\,\mathrm{J}
Entropía
La variación de entropía en el proceso reversible es
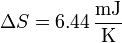
\Delta S = 6.44\,\frac{\mathrm{mJ}}{\mathrm{K}}
En el proceso reversible alternativo, la variación de entropía es naturalmente nula.
Obtenido de "http://tesla.us.es/wiki/index.php/Compresi%C3%B3n_adiab%C3%A1tica_irreversible"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 21:15, 27 may 2010. - Esta página ha sido visitada 47.456 veces. - Aviso legal - Acerca de Laplace