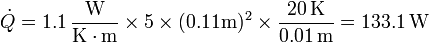Fusión de hielo en un recipiente
De Laplace
(Diferencias entre revisiones)
(→Flujo de calor) |
(→Flujo de calor) |
||
| Línea 15: | Línea 15: | ||
En este caso A es el área lateral del recipiente, <math>\Delta T</math> la diferencia de temperaturas entre las dos caras y \Delta x el espesor del recipiente. Por tanto | En este caso A es el área lateral del recipiente, <math>\Delta T</math> la diferencia de temperaturas entre las dos caras y \Delta x el espesor del recipiente. Por tanto | ||
| - | < | + | <center><math>\dot{Q}=1.1\,\frac{\mathrm{W}}{\mathrm{K}\cdot\mathrm{m}}\times 5 \times (0.11\mathrm{m})^2\times \frac{20\,\mathrm{K}}{0.01\,\mathrm{m}} = 133.1\,\mathrm{W}</math></center> |
| - | 133.1\,\mathrm{W}</math> | + | |
==Hielo fundido por segundo== | ==Hielo fundido por segundo== | ||
==Variación de entropía== | ==Variación de entropía== | ||
Revisión de 17:41 26 may 2010
Contenido |
1 Enunciado
Se tiene un bloque de hielo de 500 g de hielo sumergido en 500 g de agua, ambos a 0°C. El conjunto está contenido en un recipiente cúbico de vidrio, de 11 cm de arista interior y 1 cm de espesor (en el pequeño espacio sobrante hay aire, que se puede despreciar en el todo el problema). El recipiente está sumergido en un baño de agua a 20°C.
- Calcule la cantidad de calor que entra en el recipiente en 1 s.
- Halle la cantidad de hielo que se funde en el mismo tiempo. ¿Cuánto tiempo tardará en derretirse por completo?
- Calcule la variación de entropía en el sistema, en el ambiente y la variación de entropía total. ¿Es este proceso posible?
Datos: Conductividad térmica del vidrio 1.1 W/m·K; Entalpía específica de fusión: L_f = \Delta h_f = 333.55 kJ/kg
2 Flujo de calor
Podemos obtener la cantidad de calor que entra por segundo a partir de la expresión para la conducción de calor
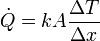
En este caso A es el área lateral del recipiente, ΔT la diferencia de temperaturas entre las dos caras y \Delta x el espesor del recipiente. Por tanto