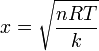Gas ideal y resorte
De Laplace
(Diferencias entre revisiones)
(→Posición de equilibrio) |
(→Posición de equilibrio) |
||
| Línea 14: | Línea 14: | ||
Llevando esto a la ecuación de los gases ideales | Llevando esto a la ecuación de los gases ideales | ||
| - | <center><math>pV = nRT\,</math>{{tose}}<math>pAx = nRT\,</math>{{tose}}<math>kx^2=nRT</math></center> | + | <center><math>pV = nRT\,</math>{{tose}}<math>pAx = nRT\,</math>{{tose}}<math>kx^2=nRT\,</math></center> |
con lo que la posición de equilibrio es | con lo que la posición de equilibrio es | ||
Revisión de 18:03 22 may 2010
Contenido |
1 Enunciado
Suponga el siguiente sistema: un cilindro de sección A y altura H se encuentra dividido en dos cámaras por un pistón móvil. En una de ellas hay n moles de un gas ideal diatómico. En la otra hay vacío. El pistón se encuentra unido al extremo del cilindro por un resorte de constante k y longitud natural H.
- Determine la posición x del pistón cuando el gas se encuentra a una temperatura T
- Teniendo en cuenta que el sistema se compone tanto del gas como del resorte, halle la energía interna del sistema.
- Suponga que se comunica una cierta cantidad de calor Q al sistema. ¿Cuál es la nueva posición del pistón? ¿Y la nueva temperatura?
- Si consideramos como sistema sólo el gas, ¿cual es su energía interna tras la absorción de calor? ¿Cuánto trabajo entra en este sistema en el proceso?
2 Posición de equilibrio
El equilibrio se alcanza cuando la fuerza sobre el pistón es nula. La fuerza es la suma de la ejercida por la presión del gas, que empuja hacia arriba, y la del resorte, que empuja hacia abajo proporcionalmente a cuánto se eleva el pistón. La condición de equilibrio es entonces

Llevando esto a la ecuación de los gases ideales
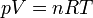

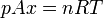

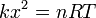
con lo que la posición de equilibrio es