Remaches de aluminio en aviones
De Laplace
(→Enunciado) |
(→Solución) |
||
| (Una edición intermedia no se muestra.) | |||
| Línea 6: | Línea 6: | ||
== Solución == | == Solución == | ||
| + | |||
| + | Llamemos <math>D_1 </math> al diámetro inicial del remache a <math>T_1 = 23 \mathrm{^oC} </math>. Entonces la sección | ||
| + | inicial del remache es | ||
| + | <center> | ||
| + | <math> | ||
| + | A_1 = \pi D_1^2/4 | ||
| + | </math> | ||
| + | </center> | ||
| + | Queremos que su diámetro sea <math>D_2=4.500\,\mathrm{mm}</math> a la temperatura de <math>T_2=-78\mathrm{^oC} </math>. Por | ||
| + | tanto, la sección a esa temperatura será | ||
| + | <center> | ||
| + | <math> | ||
| + | A_2 = \pi D_2^2/4 | ||
| + | </math> | ||
| + | </center> | ||
| + | Dado el coeficiente de dilatación líneal del aluminio, <math>\alpha=24.0\times10^{-6}\mathrm{(^oC)^{-1}} </math>, la | ||
| + | relación entre las secciones es | ||
| + | <center> | ||
| + | <math> | ||
| + | \displaystyle A_2 = A_1(1+2\alpha\Delta T) \Rightarrow \frac{\pi D_2^2}{4} = \frac{\pi D_1^2}{4}\left(1+2\alpha\Delta T\right) | ||
| + | </math> | ||
| + | </center> | ||
| + | La relación entre diámetros es | ||
| + | <center> | ||
| + | <math> | ||
| + | D_2 = D_1\sqrt{1+2\alpha\Delta T} | ||
| + | </math> | ||
| + | </center> | ||
| + | Como <math>\alpha\Delta T\ll1 </math> podemos usar el desarrollo de Taylor <math>(1+x)^n\simeq 1 + nx </math> para obtener | ||
| + | <center> | ||
| + | <math> | ||
| + | D_2 \simeq D_1(1+\alpha\Delta T) | ||
| + | </math> | ||
| + | </center> | ||
| + | Hay que señalar que llegaríamos a este mismo resultado si hubiéramos buscado desde el principio la variación del diámetro del | ||
| + | remache. | ||
| + | |||
| + | La incógnita es <math>D_1 </math>, el diámetro del remache a la temperatura <math>T_1 </math>. Entonces | ||
| + | <center> | ||
| + | <math> | ||
| + | D_1 = \frac{D_2}{1+\alpha\Delta T} = \frac{4.500\,\mathrm{mm}}{\displaystyle 1 + 24\times10^{-6}\frac{\displaystyle 1}{\displaystyle \mathrm{^oC}}(-78-23)\mathrm{^oC}}=4.511\,\mathrm{mm} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | [[Categoría:Problemas de temperatura|0]] | ||
| + | [[Categoría:Temperatura y Principio cero]] | ||
última version al 15:27 19 may 2010
1 Enunciado
Los remaches de aluminio para construcción de aviones se fabrican un poco más grandes que los
agujeros donde han de insertarse y se enfrían con hielo seco (CO2 sólido) antes de instalarse. Si el
diámetro de un agujero es 4.500 mm, ¿qué diámetro debe tener un remache a 23.0o C para que su
diámetro sea igual al del orificio cuando se enfría hasta -78.0oC, que es la temperatura del hielo seco? Suponga que el coeficiente de dilatación lineal del aluminio es constante y vale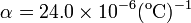 
2 Solución
Llamemos D1 al diámetro inicial del remache a T1 = 23oC. Entonces la sección inicial del remache es
Queremos que su diámetro sea 
a la temperatura de T2 = − 78oC. Por
tanto, la sección a esa temperatura será
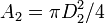
Dado el coeficiente de dilatación líneal del aluminio, 
, la
relación entre las secciones es
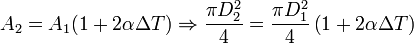
La relación entre diámetros es
Como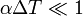 
podemos usar el desarrollo de Taylor 
para obtener
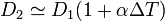
Hay que señalar que llegaríamos a este mismo resultado si hubiéramos buscado desde el principio la variación del diámetro del remache.
La incógnita es D1, el diámetro del remache a la temperatura T1. Entonces
