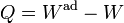Primer Principio de la Termodinámica
De Laplace
(→Trabajo) |
(→Caso general) |
||
| Línea 167: | Línea 167: | ||
:''La energía interna de un sistema aislado sobre el que no se realiza trabajo permanece constante.'' | :''La energía interna de un sistema aislado sobre el que no se realiza trabajo permanece constante.'' | ||
| - | ===Caso | + | ===Caso no adiabático=== |
| + | Supongamos ahora que se vuelve a realizar el experimento de los diferentes trabajos anteriores, pero sobre un sistema que no está aislado adiabáticamente. El resultado es ahora que ya el trabajo realizado no coincide con la variación de la energía interna. | ||
| + | |||
| + | <center><math>W \neq \Delta U</math></center> | ||
| + | |||
| + | Esto no quiere decir que en un proceso general no se pueda definir la energía interna, ya que ésta, al ser una función de estado, está perfectamente definida en cualquier caso. Lo que ocurre es que hay que añadir un término a la ecuación. | ||
| + | |||
| + | Lo que falta en este caso es la transferencia de energía en forma de calor. De esta forma, la expresión del Primer Principio queda | ||
| + | |||
| + | <center><math>W + Q = \Delta U\,</math></center> | ||
| + | |||
| + | Esta expresión no es más general que la que que dimos antes. La anterior nos sirve para definir la energía interna y nos da un procedimiento para calcularla. Esta nueva ecuación nos permite calcular el calor, conocidos el trabajo y la variación de energía interna. Otra forma equivalente de escribirlo sería | ||
| + | |||
| + | <center><math>Q = W^\mathrm{ad}-W\,</math></center> | ||
==Procesos cíclicos== | ==Procesos cíclicos== | ||
Revisión de 20:37 9 may 2010
Contenido |
1 Introducción
El principio cero de la termodinámica permite caracterizar los sistemas que se encuentran en equilibrio térmico, a través de la definición de una propiedad común que es la temperatura.
Una vez establecida esta magnitud, se trata de describir las interacciones entre un sistema y su entorno cuando se encuentran a la misma o diferente temperatura. Estas interacciones conllevan la transferencia de energía, que se manifiesta en un cambio en el estado del sistema.
Las propiedades relevantes en el intercambio energático son tres:
- Calor
- Trabajo
- Energía interna
Estas tres magnitudes se relacionan a través del primer principio de la termodinámica.
2 Calor
Definimos el calor, Q, como la transferencia de energía debida a una diferencia de temperaturas.
Si colocamos un sistema en contacto con un entorno a diferente temperatura, apreciamos que se produce un cambio en el sistema hasta que éste alcanza el equilibrio térmico con el entorno, momento en el que deja de evolucionar. En ese proceso intermedio hasta que se llega al equilibrio se ha transferido energía (del entorno hacia el sistema o al revés) en forma de calor.
El calor, por tanto, no es algo que se tiene o se almacena, sino que describe un proceso.
El calor es una función dependiente del camino, esto es, si tenemos un sistema que evoluciona desde un estado A a uno B por dos caminos diferentes, el calor intercambiado en cada uno será diferente, en general.
Para el calor se toma el criterio de signos siguiente:
- Si el calor va dese el entorno hacia el sistema se considera positivo.
- Si el calor va del sistema hacia el entorno se toma como negativo.
Cuando se estudia la termodinámica al nivel de las partículas que componen un sistema el calor está asociado a la transferencia de energía en grados de libertad microscópicos, esto es, corresponde a un cambio en la energía cinética o potencial de moléculas individuales, de forma que aunque la energía del sistema se incremente (o disminuya) lo hace de forma desorganizada.
Por tratarse de una transferencia de energía, el calor se mide en julios (J), si bien otras unidades permanecen en uso, como la caloría, siendo
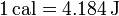
También se usa, especialmente en biología y en referencia a la alimentación, la Caloría (o caloría grande), que es en realidad una kilocaloría
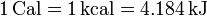
Cuando la frontera de un sistema es tal que por ella no puede pasar calor, se dice que la pared es adiabática. Si sí lo permite, se denomina pared diaterma.
Del mismo modo, un proceso en el que no se intercambia calor entre el sistema y el entorno, se denomina adiabático.
3 Trabajo
El trabajo en termodinámica es una generalización del concepto de trabajo definido en mecánica.
Supongamos el denominado experimento de Joule, en el que tenemos un recipiente de paredes adiabáticas en cuyo interior se encuentra una cierta cantidad de agua y dentro de esta una rueda de paletas. El molinillo está conectado a un eje.
El el extremo del eje podemos colocar un carrete de hilo del cual pende una cierta masa. Cuando la masa se libera y se deja caer por la acción de la gravedad, la rueda de paletas agita el agua y como consecuencia observamos un cambio de su estado (que se manifiesta en que su temperatura aumenta).
Puesto que la transferencia de energía no se debe a una diferencia de temperaturas, se dice que estamos realizando trabajo sobre el sistema. Concretamente, es un trabajo mecánico de origen gravitatorio.
Alternativamente, en lugar de una carrete y una pesa, podemos “darle cuerda” al eje, uniéndolo a un resorte de torsión, que se enrolla, cuando se libera el resorte, hace girar al eje y el molinillo, agitando el agua. De nuevo realizamos trabajo sobre el sistema, esta vez de origen elástico.
Otra posibilidad consiste en conectar el eje a un motor eléctrico, alimentado desde la red. Considerando el motor como parte del sistema, vemos que lo que introducimos en él es trabajo de origen eléctrico.
También podemos usar un motor a pilas, o un émbolo en un pistón conectado a un cigüeñal, etc. En todos los casos introducimos energía en el sistema en forma de trabajo.
Definimos entonces el trabajo, W, como la transferencia de energía no asociada a una diferencia de temperaturas.
Como con “calor” la palabra “trabajo” describe un proceso. El trabajo no se almacena, ni se tiene. Simplemente se realiza. Lo que se almacena es la energía.
El trabajo es una magnitud dependiente del camino. Dos procesos diferentes que partan del mismo estado inicial y lleguen al mismo estado final, pero por caminos diferentes, llevarán aparejados, en general, trabajos de diferente magnitud.
Como criterio de signos tomamos el establecido como estándar por la IUPAC:
- Si el trabajo se realiza por el entorno sobre el sistema, se considera positivo.
- Si el trabajo lo realiza el sistema sobre el entorno, se toma como negativo.
Hay que tener mucho cuidado, porque este criterio no es universal y de hecho, en muchos libros de termodinámica aplicada emplean justamente el opuesto. La razón es que el concepto de trabajo se desarrolló en el diseño y estudio de las máquinas, en las que lo que se desea es que el trabajo lo realice el sistema sobre el entorno.
Siendo el trabajo una forma de transferencia de energía, se mide en julios (J). Alternativamente, en sistemas de gases aparece una unidad, la atmósfera·litro, igual a
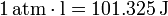
Aparte, y dependiendo del contexto, pueden aparecer diferentes unidades, como el ergio, el electrón-voltio o la BTU.
En una visión microscópica de los sistemas, el trabajo está asociado a los grados de libertad macroscópicos, esto es, al movimiento coordinado de muchas partículas.
Por ejemplo, supongamos un fluido que se empuja con un pistón. El resultado es que todas las moléculas incrementan su velocidad en la dirección y sentido en que se mueve el émbolo. Por contra, si al mismo fluido se le comunica calor, aunque cada molécula aumenta su velocidad, en promedio, la dirección en que lo hacen es aleatoria, no habiendo ningún tipo de desplazamiento conjunto.
3.1 Trabajo de expansión
Un caso particular importante es aquél en el que el trabajo sobre el sistema se realiza modificando su volumen mediante la aplicación de una presión. En este caso, el trabajo en un incremento diferencial de volumen es
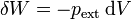
donde el signo negativo se debe al criterio de signos elegido. Si el sistema se comprime, el trabajo es positivo, pero el diferencial de volumen es negativo. El diferencial de trabajo se expresa con la letra δ para indicar que el trabajo no es una función de estado, esto es, no se trata de la variación de nada, simplemente representa una cantidad pequeña de trabajo.
La presión que aparece en la expresión anterior es la aplicada desde el exterior, que no coincidirá, en general, con la que puede tener el sistema (caso que se trate de un fluido). Es más, en general ni siquiera existirá una única presión dentro del sistema.
En el caso particular de un proceso cuasiestático, en el que el sistema evoluciona a través de estados de equilibrio, si existe una presión y además coincidirá con la aplicada, por lo que el trabajo podrá calcularse como
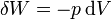 (proceso cuasiestático)
(proceso cuasiestático)El trabajo total en un proceso de expansión o compresión será
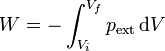
y el caso de un proceso cuasiestático
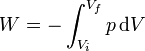 (proceso cuasiestático)
(proceso cuasiestático)Gráficamente, el trabajo en un proceso cuasiestático equivale al área bajo la curva p(V), entre el volumen inicial y final, con signo positivo si es una compresión y negativo, si es una expansión.
3.2 Trabajo eléctrico
Otro caso particular importante es el trabajo realizado por una fuente de tensión. Ésta fuente mueve cargas en el sistema, variando su tensión eléctrica en una cantidad 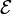 , realizando un trabajo diferencial
, realizando un trabajo diferencial
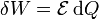
siendo el trabajo total
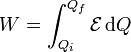
Si lo que se conoce es la cantidad de corriente que pasa por la fuente, este trabajo es igual a la integral de la potencia eléctrica respecto al tiempo
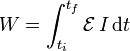
4 Primer principio de la termodinámica
4.1 Enunciado
Supongamos un sistema, como el del experimento de Joule con un tanque de agua y una rueda de paletas, que se aísla mediante paredes adiabáticas, de forma que no puede intercambiar calor con el entorno.
Se anota entonces el estado inicial del sistema (presión, temperatura, volumen, o las magnitudes que hagan falta). Se realiza un trabajo sobre este sistema, por ejemplo, soltando una pesa de un carrete, y se anota tanto el estado final como el trabajo realizado para llegar a él (en el caso de la pesa sería W = mgh).
Se quita el aislamiento y se vuelve a llevar el sistema al estado inicial. Se vuelve a aislar y se realiza trabajo, pero ahora de otro tipo, por ejemplo, calentando el sistema con una resistencia eléctrica. Cuando se llega al mismo estado final, se anota el trabajo realizado.
Se repite el proceso empleando otras formas de trabajo: elástico, químico, mediante un sistema de aire comprimido,...
El resultado empírico es que, si se parte siempre del mismo estado inicial y se llega al mismo estado final, el trabajo necesario es exactamente el mismo.
Esto constituye el Primer Principio de la Termódinámica:
- El trabajo en un proceso adiabático es independiente del camino, sólo depende de los estados inicial y final
Recordemos que, en general, el trabajo sí depende del camino. Solo en los procesos adiabáticos no lo hace.
Esto es un principio, pues no se deduce, sino que se induce de la experiencia. No se ha encontrado ningún contraejemplo de la afirmación anterior.
4.2 Energía interna
Si el trabajo adiabático es independiente del camino, podemos emplearlo para definir una función de estado, que denominaremos energía interna, U.
Para ello, partimos de un cierto estado de referencia O (con variables de estado p0, V0, T0, al cual asignamos una cierta energía U0. Para hallar la energía de otro estado A simplemente calculamos el trabajo adiabático necesario para llegar a él desde el estado de referencia
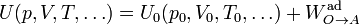
Esta energía está perfectamente definida como función de estado, ya que podemos elegir cualquier camino o cualquier tipo de trabajo para ir de O a A, que siempre resultará la misma energía interna en A.
Si ahora queremos calcular la diferencia de energías entre dos estados A y B, nos basta con imaginar un proceso que lleve de uno a otro pasando por O. Tenemos entonces
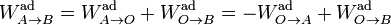
pero los dos trabajos del segundo miembro son justamente las diferencias de energía interna con el estado de referencia, por tanto
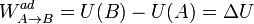
Por ello, el Primer Principio equivale a afirmar:
- Existe una función de estado, llamada energía interna, cuya variación la da el trabajo en un proceso adiabático que conecte dos estados.
En particular si tenemos un sistema aislado sobre el cual no se realiza trabajo alguno
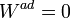

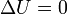
lo cual es una afirmación de la ley de conservación de la energía, equivalente al primer principio
- La energía interna de un sistema aislado sobre el que no se realiza trabajo permanece constante.
4.3 Caso no adiabático
Supongamos ahora que se vuelve a realizar el experimento de los diferentes trabajos anteriores, pero sobre un sistema que no está aislado adiabáticamente. El resultado es ahora que ya el trabajo realizado no coincide con la variación de la energía interna.
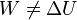
Esto no quiere decir que en un proceso general no se pueda definir la energía interna, ya que ésta, al ser una función de estado, está perfectamente definida en cualquier caso. Lo que ocurre es que hay que añadir un término a la ecuación.
Lo que falta en este caso es la transferencia de energía en forma de calor. De esta forma, la expresión del Primer Principio queda
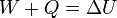
Esta expresión no es más general que la que que dimos antes. La anterior nos sirve para definir la energía interna y nos da un procedimiento para calcularla. Esta nueva ecuación nos permite calcular el calor, conocidos el trabajo y la variación de energía interna. Otra forma equivalente de escribirlo sería