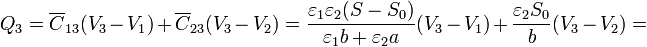Microtira situada entre dos placas
De Laplace
(Nueva página: ==Enunciado== Sobre una placa metálica plana, de sección <math>S</math> (que supondremos en <math>z=0</math>), se coloca una capa de dieléctrico de permitividad <math>\varepsilon_1...) |
|||
| Línea 4: | Línea 4: | ||
Si las placas inferior, intermedia y superior se colocan, respectivamente, a potenciales <math>V_1</math>, <math>V_2</math> y <math>V_3</math>, ¿Cuánto vale la carga (libre) almacenada en cada conductor? Desprecie totalmente los efectos de borde (suponiendo <math>\mathbf{E}=E\mathbf{u}_{z}</math>) y los posibles campos exteriores al sistema. | Si las placas inferior, intermedia y superior se colocan, respectivamente, a potenciales <math>V_1</math>, <math>V_2</math> y <math>V_3</math>, ¿Cuánto vale la carga (libre) almacenada en cada conductor? Desprecie totalmente los efectos de borde (suponiendo <math>\mathbf{E}=E\mathbf{u}_{z}</math>) y los posibles campos exteriores al sistema. | ||
| + | ==Solución== | ||
| + | La forma más simple de abordar este problema es por medio del circuito equivalente. | ||
| + | |||
| + | La configuración del sistema permite dividir el espacio entre las placas en cuatro regiones: | ||
| + | |||
| + | <ol type=I> | ||
| + | <li> La región de sección $S_0$ y espesor $a$, comprendida entre la placa inferior y la región intermedia.</li> | ||
| + | <li> La de sección $S_0$ y espesor $b$, situada entre la placa intermedia y la superior.</li> | ||
| + | <li> La de sección $S-S_0$ y espesor $a$ situada entre la placa inferior y la interfaz entre los dos dieléctricos. Nótese que esta región comprende las partes del dieléctrico situadas a izquierda y derecha de la placa intermedia, ya que son completamente análogas.</li> | ||
| + | <li> La de sección $S-S_0$ situada entre la interfaz y la placa superior.</li> | ||
| + | </ol> | ||
| + | |||
| + | |||
| + | Si despreciamos completamente los efectos de borde en el sistema y consideramos que el campo en cada una de las regiones va en la dirección $\mathbf{u}_{z}$, cada zona se comporta como un condensador de placas planas y paralelas, siendo las respectivas capacidades | ||
| + | |||
| + | <center><math>C_\mathrm{I} = \frac{\varepsilon_1S_0}{a}</math>{{qquad}}{{qquad}}<math>C_\mathrm{II} = \frac{\varepsilon_2S_0}{b}</math>{{qquad}}{{qquad}} <math>C_\mathrm{III}= \frac{\varepsilon_1(S-S_0)}{a}</math>{{qquad}}{{qquad}}<math>C_\mathrm{IV}= \frac{\varepsilon_2(S-S_0)}{b}</math></center> | ||
| + | |||
| + | El circuito equivalente al sistema está formado en primer lugar, por un nodo que representa a cada conductor. Llamaremos nodo $1$ a la placa inferior, $2$ a la intermedia, y $3$ a la superior. Entre los nodos $1$ y $2$ se encuentra el condensador $C_\mathrm{I}$, mientras que el $C_\mathrm{II}$ se encuentra situado entre el conductor $2$ y el $3$. Entre las placas $1$ y $3$ el condensador está formado por una | ||
| + | asociación en serie de los condensadores $C_\mathrm{III}$ y $C_\mathrm{IV}$. | ||
| + | |||
| + | Con esto tenemos la siguientes capacidades | ||
| + | |||
| + | <center><math>\overline{C}_{12}= \frac{\varepsilon_1S_0 }{a}</math>{{qquad}}{{qquad}}<math>\overline{C}_{23}= \frac{\varepsilon_2S_0 }{b}</math>{{qquad}}<math>\overline{C}_{13}= \frac{C_\mathrm{III}C_\mathrm{IV}}{C_\mathrm{III}+C_\mathrm{IV}}= \frac{\varepsilon_1\varepsilon_2(S-S_0) }{\varepsilon_1b+\varepsilon_1a}</math></center> | ||
| + | |||
| + | Las autocapacidades <math>\overline{C}_{ii}</math> son todas nulas, ya que despreciamos los campos exteriores al sistema. | ||
| + | |||
| + | Estas capacidades pueden determinarse detalladamente como se indica en otros problemas. | ||
| + | |||
| + | Con esto, resultan las relaciones entre las cargas y los potenciales. Para la placa inferior tenemos | ||
| + | |||
| + | <center><math>Q_1=\overline{C}_{12} (V_1-V_2) + \overline{C}_{13}(V_1-V_3) = | ||
| + | \frac{\varepsilon_1S_0}{a}(V_1-V_2)+\frac{\varepsilon_1\varepsilon_2(S-S_0)}{\varepsilon_1b+\varepsilon_2a}(V_1-V_3)=</math> | ||
| + | <math>\left(\frac{\varepsilon_1S_0}{a}+\frac{\varepsilon_1\varepsilon_2(S-S_0)}{\varepsilon_1b+\varepsilon_2a}\right)V_1 | ||
| + | -\left(\frac{\varepsilon_1S_0}{a}\right)V_2-\left(\frac{\varepsilon_1\varepsilon_2(S-S_0)}{\varepsilon_1b+\varepsilon_2a}\right)V_3 | ||
| + | </math></center> | ||
| + | |||
| + | Para la intermedia | ||
| + | |||
| + | <center><math>Q_2=\overline{C}_{12} (V_2-V_1) + \overline{C}_{23}(V_2-V_3) = \frac{\varepsilon_1S_0}{a}(V_2-V_1)+\frac{\varepsilon_2S_0}{b}(V_2-V_3)=</math><math>-\left(\frac{\varepsilon_1S_0}{a}\right)V_1 | ||
| + | +\left(\frac{\varepsilon_1S_0}{a}+\frac{\varepsilon_2S_0}{b}\right)V_2- | ||
| + | \left(\frac{\varepsilon_2S_0}{b}\right)V_3</math></center> | ||
| + | |||
| + | Y para la superior | ||
| + | |||
| + | <center><math>Q_3=\overline{C}_{13} (V_3-V_1) + \overline{C}_{23}(V_3-V_2) = | ||
| + | \frac{\varepsilon_1\varepsilon_2(S-S_0)}{\varepsilon_1b+\varepsilon_2a}(V_3-V_1)+\frac{\varepsilon_2S_0}{b}(V_3-V_2)=</math><math>-\left(\frac{\varepsilon_1\varepsilon_2(S-S_0)}{\varepsilon_1b+\varepsilon_2a}\right)V_1 | ||
| + | -\left(\frac{\varepsilon_2S_0}{b}\right)V_2 | ||
| + | +\left(\frac{\varepsilon_1\varepsilon_2(S-S_0)}{\varepsilon_1b+\varepsilon_2a}+\frac{\varepsilon_2S_0}{b}\right)V_3</math></center> | ||
[[Categoría:Problemas de materiales dieléctricos]] | [[Categoría:Problemas de materiales dieléctricos]] | ||
Revisión de 12:12 4 may 2010
1 Enunciado
Sobre una placa metálica plana, de sección S (que supondremos en z = 0), se coloca una capa de dieléctrico de permitividad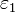 
con espesor a. Sobre esta capa se sitúa una lámina metálica, de sección S0 < S, el resto de la superficie se deja libre y descargado. Se superpone una segunda capa de dieléctrico de permitividad 
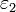y espesor b. Por último, el sistema se cierra con una segunda lámina metálica de sección S.
Si las placas inferior, intermedia y superior se colocan, respectivamente, a potenciales V1, V2 y V3, ¿Cuánto vale la carga (libre) almacenada en cada conductor? Desprecie totalmente los efectos de borde (suponiendo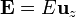 
) y los posibles campos exteriores al sistema.
2 Solución
La forma más simple de abordar este problema es por medio del circuito equivalente.
La configuración del sistema permite dividir el espacio entre las placas en cuatro regiones:
- La región de sección $S_0$ y espesor $a$, comprendida entre la placa inferior y la región intermedia.
- La de sección $S_0$ y espesor $b$, situada entre la placa intermedia y la superior.
- La de sección $S-S_0$ y espesor $a$ situada entre la placa inferior y la interfaz entre los dos dieléctricos. Nótese que esta región comprende las partes del dieléctrico situadas a izquierda y derecha de la placa intermedia, ya que son completamente análogas.
- La de sección $S-S_0$ situada entre la interfaz y la placa superior.
Si despreciamos completamente los efectos de borde en el sistema y consideramos que el campo en cada una de las regiones va en la dirección $\mathbf{u}_{z}$, cada zona se comporta como un condensador de placas planas y paralelas, siendo las respectivas capacidades
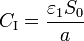
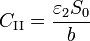
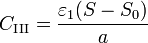
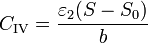
El circuito equivalente al sistema está formado en primer lugar, por un nodo que representa a cada conductor. Llamaremos nodo $1$ a la placa inferior, $2$ a la intermedia, y $3$ a la superior. Entre los nodos $1$ y $2$ se encuentra el condensador $C_\mathrm{I}$, mientras que el $C_\mathrm{II}$ se encuentra situado entre el conductor $2$ y el $3$. Entre las placas $1$ y $3$ el condensador está formado por una asociación en serie de los condensadores $C_\mathrm{III}$ y $C_\mathrm{IV}$.
Con esto tenemos la siguientes capacidades
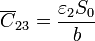
Las autocapacidades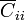 
son todas nulas, ya que despreciamos los campos exteriores al sistema.
Estas capacidades pueden determinarse detalladamente como se indica en otros problemas.
Con esto, resultan las relaciones entre las cargas y los potenciales. Para la placa inferior tenemos
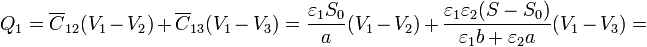
Para la intermedia
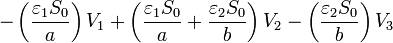
Y para la superior
