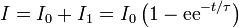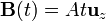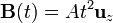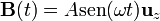Espira circular en un campo variable
De Laplace
(→Campo en rampa) |
(→Solución) |
||
| Línea 37: | Línea 37: | ||
En el primer caso, el campo varía uniformemente, por lo que su derivada es una constante y la ecuación diferencial se reduce a | En el primer caso, el campo varía uniformemente, por lo que su derivada es una constante y la ecuación diferencial se reduce a | ||
| - | <center><math></math></center> | + | <center><math>L\frac{\mathrm{d}I}{\mathrm{d}t}+IR=-A\pi a^2</math></center> |
| + | |||
| + | esto es, la f.e.m. externa equivale a un generador de corriente continua. | ||
| + | |||
| + | Si esta variación lleva establecida mucho tiempo, podemos suponer que el periodo transitorio inicial ha finalizado y se ha alcanzado el estado estacionario. | ||
| + | |||
| + | Suponiendo una intensidad constante queda | ||
| + | |||
| + | <center><math>0 + I_0R=-A\pi a^2</math></center> | ||
| + | |||
| + | <center><math>I_0=-\frac{A\pi a^2}{R}</math></center> | ||
| + | |||
| + | Si el campo está aumentando, la corriente es tal que su campo se opone al aumento del flujo externo, de acuerdo con la ley de Lenz. | ||
===Campo en rampa a partir de t=0=== | ===Campo en rampa a partir de t=0=== | ||
| + | En el apartado anterior hemos despreciado el efecto del transitorio inicial. Para ver cuándo podemos hacer esta aproximación, y para describir el comportamiento del sistema en este transitorio, supongamos que el campo variable no lleva mucho tiempo aplicado, sino que comienza en t=0 y que antes de su aplicación no circula corriente por la espira. | ||
| + | |||
| + | En este caso tenemos de nuevo la ecuación diferencial | ||
| + | |||
| + | <center><math>L\frac{\mathrm{d}I}{\mathrm{d}t}+IR=-A\pi a^2</math></center> | ||
| + | |||
| + | pero ahora con la condición inicial | ||
| + | |||
| + | <center><math>I(t=0)=0\,</math></center> | ||
| + | |||
| + | por lo que la solución estacionaria que calculamos no puede ser la solución del problema, ya que no verifica la condición inicial. Si consideramos que la corriente debe ser la suma de la estacionaria más una corrección nos queda | ||
| + | |||
| + | <center><math>I(t)=I_0 + I_1(t)\,</math></center> | ||
| + | |||
| + | <center><math>I_1(t=0)=-I_0\,\,</math></center> | ||
| + | |||
| + | <center><math>L\frac{\mathrm{d}I_1}{\mathrm{d}t}+I_1R=0</math></center> | ||
| + | |||
| + | (ya que el segundo miembro se cancela con el término <math>RI_0\,</math>). La solución de esta ecuación es | ||
| + | |||
| + | <center><math>I_1 = -I_0 \mathrm{ee}^{-t/\tau}\qquad\qquad \tau = \frac{L}{R}</math></center> | ||
| + | |||
| + | y la solución de la ecuación completa | ||
| + | |||
| + | <center><math>I = I_0 + I_1 =I_0\left(1 - \mathrm{ee}^{-t/\tau}\right)</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | |||
===Campo con variación parabólica=== | ===Campo con variación parabólica=== | ||
===Campo sinusoidal=== | ===Campo sinusoidal=== | ||
[[Categoría:Problemas de inducción electromagnética]] | [[Categoría:Problemas de inducción electromagnética]] | ||
Revisión de 19:16 24 may 2008
Contenido |
1 Enunciado
Una espira circular de radio  , con autoinducción
, con autoinducción  y resistencia
y resistencia  , se encuentra sometida a un campo magnético uniforme en el espacio pero variable en el tiempo. El campo es perpendicular al plano de la espira.
, se encuentra sometida a un campo magnético uniforme en el espacio pero variable en el tiempo. El campo es perpendicular al plano de la espira.
Calcule la corriente que circula por la espira si el campo magnético varía en el tiempo, durante un largo intervalo, como
2 Solución
2.1 Planteamiento general
En todos los casos por la espira circula una corriente debida a la presencia de una fuerza electromotriz causada por el cambio en el flujo magnético
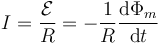
Este flujo magnético es la superposición de dos contribuciones: la debida al campo externo y la debida a la propia espira. Ésta última es proporcional a la corriente que circula por la espira
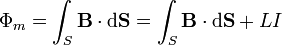
lo que da la ecuación diferencial
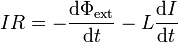
o, reordenando términos
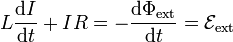
En términos del circuito equivalente, este sencillo sistema equivale a tres elementos de circuito: una resistencia R, una autoinducción L y un generador de f.e.m. 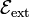 .
.
En todos los casos de este problema, el campo magnético externo es uniforme, aunque dependiente del tiempo. Por ello, el flujo magnético y la fuerza electromotriz externa valen
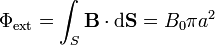
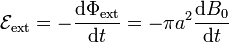
2.2 Campo en rampa
En el primer caso, el campo varía uniformemente, por lo que su derivada es una constante y la ecuación diferencial se reduce a

esto es, la f.e.m. externa equivale a un generador de corriente continua.
Si esta variación lleva establecida mucho tiempo, podemos suponer que el periodo transitorio inicial ha finalizado y se ha alcanzado el estado estacionario.
Suponiendo una intensidad constante queda
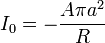
Si el campo está aumentando, la corriente es tal que su campo se opone al aumento del flujo externo, de acuerdo con la ley de Lenz.
2.3 Campo en rampa a partir de t=0
En el apartado anterior hemos despreciado el efecto del transitorio inicial. Para ver cuándo podemos hacer esta aproximación, y para describir el comportamiento del sistema en este transitorio, supongamos que el campo variable no lleva mucho tiempo aplicado, sino que comienza en t=0 y que antes de su aplicación no circula corriente por la espira.
En este caso tenemos de nuevo la ecuación diferencial

pero ahora con la condición inicial
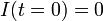
por lo que la solución estacionaria que calculamos no puede ser la solución del problema, ya que no verifica la condición inicial. Si consideramos que la corriente debe ser la suma de la estacionaria más una corrección nos queda
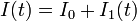
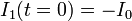
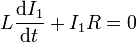
(ya que el segundo miembro se cancela con el término 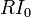 ). La solución de esta ecuación es
). La solución de esta ecuación es
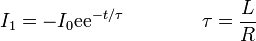
y la solución de la ecuación completa