Entrar Página Discusión Historial Go to the site toolbox

Pulso en una cuerda

De Laplace

(Diferencias entre revisiones)
(→Solución)
(→Solución)
Línea 19: Línea 19:
<center><math>K=\frac{1}{v^2}</math>{{tose}} <math>v = \frac{1}{\sqrt{K}}</math></center>
<center><math>K=\frac{1}{v^2}</math>{{tose}} <math>v = \frac{1}{\sqrt{K}}</math></center>
-
Antes de empezar a derivar, podemos obtener una expresión sin decimales si expresamos x en milímetros, lo que equivale a multiplicar el valor de x por 10 y escribir la elongación como
+
Antes de empezar a derivar, podemos obtener una expresión sin decimales si empleamos fracciones y escribimos la elongación como
-
<center><math>y = \frac{1}{x^2-6tx+9t^2+1}\qquad (y\ \mbox{en cm},\ x\ \mbox{en mm})</math></center>
+
<center><math>y = \frac{1}{x^2/100-6tx/10+9t^2+1}=\frac{100}{x^2-60tx+900t^2+100}</math></center>
Derivando una vez respecto a la posición
Derivando una vez respecto a la posición
-
<center><math>\frac{\partial y}{\partial x}=-\frac{2x-6t}{(x^2-6tx+9t^2+1)^2}</math></center>
+
<center><math>\frac{\partial y}{\partial x}=-\frac{100(2x-60t}{(x^2-60tx+900t^2+10)^2}</math></center>
Derivando una segunda vez
Derivando una segunda vez
-
<center><math>\frac{\partial^2 y}{\partial x^2}=-\frac{2(x^2-6tx+9t^2+1)-2(2x-6t)^2}{(x^2-6tx+9t^2+1)^3}</math></center>
+
<center><math>\frac{\partial^2 y}{\partial x^2}=-\frac{100(2)(x^2-60tx+900t^2+100)-100(2)(2x-6t)^2}{(x^2-60tx+900t^2+100)^3}</math></center>
Agrupando términos
Agrupando términos
-
<center><math>\frac{\partial^2 y}{\partial x^2}=\frac{2(3x^2-18xt+27t^2-1)}{(x^2-6tx+9t^2+1)^3}</math></center>
+
<center><math>\frac{\partial^2 y}{\partial x^2}=\frac{200(3x^2-180xt+2700t^2-100)}{(x^2-60tx+900t^2+100)^3}</math></center>
Derivando ahora respecto al tiempo
Derivando ahora respecto al tiempo
-
<center><math>\frac{\partial y}{\partial t}=-\frac{-6x+18t}{(x^2-6tx+9t^2+1)^2}</math></center>
+
<center><math>\frac{\partial y}{\partial t}=-\frac{100(-60x+1800t)}{(x^2-60tx+900t^2+100)^2}</math></center>
Derivando de nuevo
Derivando de nuevo
-
<center><math>\frac{\partial^2 y}{\partial t^2}=-\frac{18(x^2-6tx+9t^2+1)-2(2x-6t)^2}{(x^2-6tx+9t^2+1)^3}</math></center>
+
<center><math>\frac{\partial^2 y}{\partial t^2}=-\frac{100(1800)(x^2-60tx+900t^2+100)-100(2)(-60x-1800t)^2}{(x^2-6tx+9t^2+1)^3}</math></center>
Agrupando términos
Agrupando términos
-
<center><math>\frac{\partial^2 y}{\partial t^2}=\frac{18(3x^2-18xt+27t^2-1)}{(x^2-6tx+9t^2+1)^3}</math></center>
+
<center><math>\frac{\partial^2 y}{\partial t^2}=\frac{180000(3x^2-180xt+2700t^2-100)}{(x^2-60tx+900t^2+100)^3}</math></center>
Comparando esta expresión con la segunda derivada respecto al tiempo vemos que son efectivamente proporcionales, cumpliéndose que
Comparando esta expresión con la segunda derivada respecto al tiempo vemos que son efectivamente proporcionales, cumpliéndose que
-
<center><math>\frac{\partial^2 y}{\partial x^2}=\frac{1}{9}\frac{\partial^2 y}{\partial x^2}</math></center>
+
<center><math>\frac{\partial^2 y}{\partial x^2}=\frac{200}{180000}\frac{\partial^2 y}{\partial x^2}</math></center>
y por tanto la velocidad de la onda es
y por tanto la velocidad de la onda es
-
<center><math>v= \sqrt{9}= 3\,\frac{\mathrm{mm}}{\mathrm{s}}=0.3\,\frac{\mathrm{cm}}{\mathrm{s}}</math></center>
+
<center><math>v= \sqrt{900}= 30\,\frac{\mathrm{cm}}{\mathrm{s}}}</math></center>
Las unidades de <math>v</math> salen de dividir las unidades en las que medimos la coordenada <math>x</math> entre las que usamos para el tiempo.
Las unidades de <math>v</math> salen de dividir las unidades en las que medimos la coordenada <math>x</math> entre las que usamos para el tiempo.
Línea 59: Línea 59:
También podíamos haber llegado a este resultado por inspección, observando que el pulso se puede escribir en la forma
También podíamos haber llegado a este resultado por inspección, observando que el pulso se puede escribir en la forma
-
<center><math>y = \frac{1}{(x-3t)^2+1}\qquad (x\ \mbox{en mm}) </math></center>
+
<center><math>y = \frac{100}{(x-30t)^2+100}</math></center>
-
o si no cambiamos las unidades de x y empleamos la expresión original
+
que es un caso particular de la forma general
-
<center><math>y = \frac{1}{(0.1x-3t)^2+1}\qquad (x\ \mbox{en mm}) </math></center>
+
<center><math>y = f(x-vt)\,</math></center>
 +
si hacemos
 +
 +
<center><math>v = 30\,\frac{\mathrm{cm}}{\mathrm{s}}}</math>{{qquad}}{{qquad}}<math>f(s)=\frac{100}{s^2+1}</math></center>
 +
 +
Por tratarse de una función de esta forma, automáticamente satisface la [[ecuación de onda]] y su velocidad es la constante <math>v</math> = 30&thinsp;m/s.
[[Categoría:Problemas de movimiento ondulatorio]]
[[Categoría:Problemas de movimiento ondulatorio]]

Revisión de 21:16 26 mar 2010

1 Enunciado

Los puntos de una cuerda horizontal se mueven verticalmente, de forma que el perfil de la cuerda tiene la forma

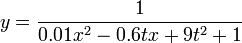
y = \frac{1}{0.01x^2-0.6tx+9t^2+1}

donde x e y se miden en centímetros y t en segundos.

  1. Halle la velocidad de esta onda.
  2. Demuestre que esta señal cumple la ecuación de onda.
  3. Calcule la velocidad del punto de la cuerda situado en x = 15 cm, en (a) t = 0 s, (b) t = 0.5 s, (c) t = 1 s.

2 Solución

Podemos resolver los dos primeros apartados simultáneamente. Si calculamos la segunda derivada respecto a x la segunda derivada respecto a t y obtenemos que ambas son proporcionales

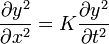
\frac{\partial y^2}{\partial x^2}=K\frac{\partial y^2}{\partial t^2}

entonces podemos afirmar que verifica la ecuación de onda y además que

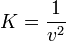
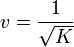
K=\frac{1}{v^2}   \Rightarrow    v = \frac{1}{\sqrt{K}}

Antes de empezar a derivar, podemos obtener una expresión sin decimales si empleamos fracciones y escribimos la elongación como

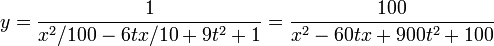
y = \frac{1}{x^2/100-6tx/10+9t^2+1}=\frac{100}{x^2-60tx+900t^2+100}

Derivando una vez respecto a la posición

\frac{\partial y}{\partial x}=-\frac{100(2x-60t}{(x^2-60tx+900t^2+10)^2}

Derivando una segunda vez

\frac{\partial^2 y}{\partial x^2}=-\frac{100(2)(x^2-60tx+900t^2+100)-100(2)(2x-6t)^2}{(x^2-60tx+900t^2+100)^3}

Agrupando términos

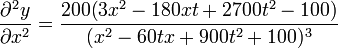
\frac{\partial^2 y}{\partial x^2}=\frac{200(3x^2-180xt+2700t^2-100)}{(x^2-60tx+900t^2+100)^3}

Derivando ahora respecto al tiempo

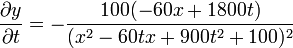
\frac{\partial y}{\partial t}=-\frac{100(-60x+1800t)}{(x^2-60tx+900t^2+100)^2}

Derivando de nuevo

\frac{\partial^2 y}{\partial t^2}=-\frac{100(1800)(x^2-60tx+900t^2+100)-100(2)(-60x-1800t)^2}{(x^2-6tx+9t^2+1)^3}

Agrupando términos

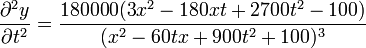
\frac{\partial^2 y}{\partial t^2}=\frac{180000(3x^2-180xt+2700t^2-100)}{(x^2-60tx+900t^2+100)^3}

Comparando esta expresión con la segunda derivada respecto al tiempo vemos que son efectivamente proporcionales, cumpliéndose que

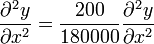
\frac{\partial^2 y}{\partial x^2}=\frac{200}{180000}\frac{\partial^2 y}{\partial x^2}

y por tanto la velocidad de la onda es

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): v= \sqrt{900}= 30\,\frac{\mathrm{cm}}{\mathrm{s}}}

Las unidades de v salen de dividir las unidades en las que medimos la coordenada x entre las que usamos para el tiempo.

También podíamos haber llegado a este resultado por inspección, observando que el pulso se puede escribir en la forma

y = \frac{100}{(x-30t)^2+100}

que es un caso particular de la forma general

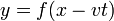
y = f(x-vt)\,

si hacemos

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): v = 30\,\frac{\mathrm{cm}}{\mathrm{s}}}         f(s)=\frac{100}{s^2+1}

Por tratarse de una función de esta forma, automáticamente satisface la ecuación de onda y su velocidad es la constante v = 30 m/s.

Obtenido de "http://tesla.us.es/wiki/index.php/Pulso_en_una_cuerda"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace