Pulso en una cuerda
De Laplace
(Diferencias entre revisiones)
| Línea 29: | Línea 29: | ||
Derivando una segunda vez | Derivando una segunda vez | ||
| - | <center><math>\frac{\partial^2 y}{\partial x^2}=-\frac{ | + | <center><math>\frac{\partial^2 y}{\partial x^2}=-\frac{2(x^2-6tx+9t^2+1)-2(2x-6t)^2}{(x^2-6tx+9t^2+1)^3}</math></center> |
Agrupando términos | Agrupando términos | ||
| - | <center><math>\frac{\partial^2 y}{\partial x^2}= | + | <center><math>\frac{\partial^2 y}{\partial x^2}=\frac{2(3x^2-18xt+27t^2-1)}{(x^2-6tx+9t^2+1)^3}</math></center> |
[[Categoría:Problemas de movimiento ondulatorio]] | [[Categoría:Problemas de movimiento ondulatorio]] | ||
Revisión de 20:34 26 mar 2010
1 Enunciado
Los puntos de una cuerda horizontal se mueven verticalmente, de forma que el perfil de la cuerda tiene la forma
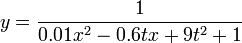
donde x e y se miden en centímetros y t en segundos.
- Halle la velocidad de esta onda.
- Demuestre que esta señal cumple la ecuación de onda.
- Calcule la velocidad del punto de la cuerda situado en x = 15 cm, en (a) t = 0 s, (b) t = 0.5 s, (c) t = 1 s.
2 Solución
Podemos resolver los dos primeros apartados simultáneamente. Si calculamos la segunda derivada respecto a x la segunda derivada respecto a t y obtenemos que ambas son proporcionales
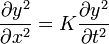
entonces podemos afirmar que verifica la ecuación de onda y además que
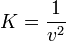

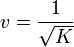
Antes de empezar a derivar, podemos obtener una expresión sin decimales si expresamos x en milímetros, lo que equivale a multiplicar el valor de x por 10 y escribir la elongación como

Derivando una vez respecto a la posición

Derivando una segunda vez

Agrupando términos






