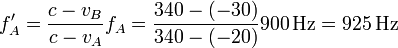Efecto Doppler de dos vehículos
De Laplace
(→Frecuencia de los batidos) |
(→Señales que llegan al otro conductor) |
||
| Línea 35: | Línea 35: | ||
==Señales que llegan al otro conductor== | ==Señales que llegan al otro conductor== | ||
| + | ===Al coche de bomberos=== | ||
| + | El conductor del coche de bomberos funciona como un [[Efecto_Doppler#Caso_de_que_los_dos_est.C3.A9n_en_movimiento|observador móvil]] que recibe señales desde una fuente (la ambulancia) también en movimiento. | ||
| + | |||
| + | El coche de bomberos (receptor) se mueve hacia la ambulancia (emisor), por lo que su velocidad es negativa. La ambulancia se mueve alejándose del punto donde se encontraba el coche de bomberos, por lo que su velocidad también es negativa. Esto da una frecuencia recibida de | ||
| + | |||
| + | <center><math>f'_A = \frac{c-v_B}{c-v_A}f_A = \frac{340-(-30)}{340-(-20)}900\,\mathrm{Hz} = 925\,\mathrm{Hz}</math></center> | ||
| + | |||
==Señales dos minutos después== | ==Señales dos minutos después== | ||
[[Categoría:Problemas de ondas sonoras]] | [[Categoría:Problemas de ondas sonoras]] | ||
Revisión de 14:38 26 mar 2010
Contenido |
1 Enunciado
Al lugar de un incendio acuden por la misma carretera rectilínea, en el mismo sentido, un coche de bomberos a 108 km/h y una ambulancia de 72 km/h. El coche de bomberos usa una sirena de 880 Hz, mientras que la ambulancia emplea una de 900 Hz.
- En un momento dado el coche de bomberos se encuentra a 4 km del lugar del incendio, y la ambulancia a 3.00 km de él y ambos vehículos hacen sonar sus sirenas. Para una persona situada en el camino de los vehículos, pero 1 km antes del lugar del incendio, ¿cuál de los dos sonidos emitidos en ese instante llega antes?, ¿qué sirena suena más aguda?, ¿en cuántos hercios? ¿Cuál es la frecuencia de la señal y de los batidos que oye esa persona?
- Para el conductor de la ambulancia y el del coche de bomberos, ¿cuál es la frecuencia que le llega del otro vehículo cuando se encuentran en la posición del apartado anterior?
- A los 2 minutos ambos vehículos hacen sonar sus sirenas otra vez. ¿cómo quedan los dos resultados de los dos apartados anteriores?
Supóngase la velocidad del sonido c = 340 m/s.
2 Señales que llegan a un observador en reposo
2.1 Del coche de bomberos
El coche de bomberos se acerca al observador en reposo con una velocidad
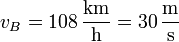
Al tratarse de una fuente en movimiento que se acerca a un observador en reposo la frecuencia que éste percibe es
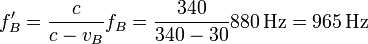
2.2 De la ambulancia
La ambulancia se acerca igualmente al observador, aunque a una velocidad menor
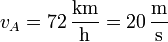
Al tratarse de nuevo de una fuente en movimiento que se acerca a un receptor en reposo la frecuencia que el observador recibe es
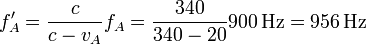
Vemos que aunque la ambulancia emite a una frecuencia mayor que el coche de bomberos, como consecuencia del efecto Doppler, el observador recibe una frecuencia mayor procedente de la ambulancia que de los bomberos.
2.3 Frecuencia de los batidos
Al llegar al observador dos señales de frecuencias próximas, su superposición produce batidos o pulsaciones en el sonido resultante. La frecuencia de estos batidos es
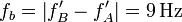
3 Señales que llegan al otro conductor
3.1 Al coche de bomberos
El conductor del coche de bomberos funciona como un observador móvil que recibe señales desde una fuente (la ambulancia) también en movimiento.
El coche de bomberos (receptor) se mueve hacia la ambulancia (emisor), por lo que su velocidad es negativa. La ambulancia se mueve alejándose del punto donde se encontraba el coche de bomberos, por lo que su velocidad también es negativa. Esto da una frecuencia recibida de