Sonar de un murciélago
De Laplace
(→Solución) |
|||
| Línea 35: | Línea 35: | ||
<math> | <math> | ||
v_m=c\frac{\Delta f}{2f_0+\Delta f}=\frac{c\Delta f}{2f_0}\left(1+\frac{\Delta f}{2f_0}\right)^{-1}\simeq | v_m=c\frac{\Delta f}{2f_0+\Delta f}=\frac{c\Delta f}{2f_0}\left(1+\frac{\Delta f}{2f_0}\right)^{-1}\simeq | ||
| - | \frac{c\Delta f}{2f_0}(1-\frac{\Delta f}{2f_0}) | + | \frac{c\Delta f}{2f_0}\left(1-\frac{\Delta f}{2f_0}) |
</math> | </math> | ||
</center> | </center> | ||
| Línea 73: | Línea 73: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | d_0=\frac{(c+ | + | d_0=\frac{\left(c+v_mμ\right)\Delta t}{2}=\frac{c\Delta t}{2}\left(1+\frac{\Delta f}{f_1+f_0}\right)\simeq |
| - | \frac{c\Delta t}{2}(1+\frac{\Delta f}{2f_0}) | + | \frac{c\Delta t}{2}\left(1+\frac{\Delta f}{2f_0}\right) |
</math> | </math> | ||
</center> | </center> | ||
| Línea 82: | Línea 82: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | d_2=d_0-v_m\Delta t=\frac{c-v_m}{2}\Delta t=\frac{c\Delta t}{2}(1-\frac{\Delta f}{f_1+f_0})\simeq | + | d_2=d_0-v_m\Delta t=\frac{c-v_m}{2}\Delta t=\frac{c\Delta t}{2}\left(1-\frac{\Delta f}{f_1+f_0}\right)\simeq |
| - | \frac{c\Delta t}{2}(1-\frac{\Delta f}{2f_0}) | + | \frac{c\Delta t}{2}\left(1-\frac{\Delta f}{2f_0}\right) |
</math> | </math> | ||
</center> | </center> | ||
Revisión de 11:29 19 mar 2010
1 Enunciado
Un murciélago que vuela hacia una pared emite un ultrasonido de frecuencia f0. Recibe el eco un tiempo Δt más tarde y con una frecuencia f1. Determine la velocidad con la que se mueve el murciélago y la distancia a la que se encuentra de la pared en el momento de recibir el eco. (Dato: c = 343 m/s)
2 Solución
Vamos a calcular en primer lugar la velocidad del murciélago utlizando el corrimiento de frecuencias debido al efecto Doppler. El murciélago emite un sonido con frecuencia f0. Esta onda llega a la pared, donde rebota y es emitida hacia el murciélago con una frecuencia fp. Finalmente este sonido llega al murciélago con una frecuencia f1.
En el primer proceso la pared actúa como receptor y el murciélago como emisor. Así pues la frecuencia que percibe la pared es
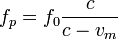
La velocidad vm se considera positiva pues el murciélago se acerca a la pared.
El sonido proviniente de la pared tiene frecuencia fp. Al llegar al murciélago, éste es el receptor y la pared es el emisor. Así pues la frecuencia que percibe el animal es
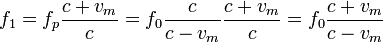
Despejando obtenemos la velocidad del murciélago en función de las frecuencias y la velocidad del sonido en el aire
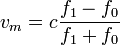
La velocidad del murciélago siempre será mucho menor que la del sonido en el aire. Entonces las frecuencias f0 y
f1 son muy parecidas. Se cumple por tanto, 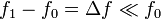 . Obtenemos así una
expresión más sencilla de la velocidad del murciélago
. Obtenemos así una
expresión más sencilla de la velocidad del murciélago
No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): v_m=c\frac{\Delta f}{2f_0+\Delta f}=\frac{c\Delta f}{2f_0}\left(1+\frac{\Delta f}{2f_0}\right)^{-1}\simeq \frac{c\Delta f}{2f_0}\left(1-\frac{\Delta f}{2f_0})
Vamos a calcular ahora la distancia a la que estaba el murciélago de la pared cuando emitió el sonido. Consideramos tres instantes de tiempo como se indica en la figura. En t = 0 el murciélago está a una distancia d0 de la pared y emite el ultrasonido. En t = Δt1 el ultrasonido llega a la pared y rebota. En ese momento el murciélago está a la distancia d1 de la pared. Finalmente, el ultrasonido emitido por la pared llega al murciélago en el instante Δt, estando el animal a la distancia d2 del muro.
Durante el tiempo Δt el murciélago ha seguido avanzando hacia la pared con velocidad vm. Por
tanto, cuando recibe el ultrasonido la distancia d2 es
d2 = d0 − vmΔt
Tenemos que calcular d0. Para ello vemos que los intervalos de tiempo Δt1 y Δt2 valen
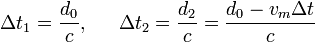
Sumando los dos tenemos
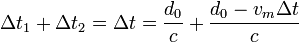
Despejando d0 queda
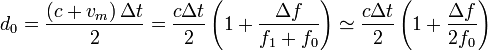
Observemos que si el murciélago no se mueve, tenemos Δf = 0 y por tanto d0 = cΔt / 2.
Finalmente, la distancia pedida es
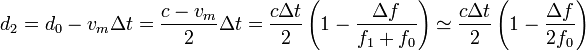
De nuevo podemos comprobar que si Δf = 0, se tiene d2 = cΔt / 2, como es lógico.
Los murciélagos se desplazan con velocidades alrededor de 5 m/s. Podemos estimar el desplazamiento de frecuencias que produce
esta velocidad. De la expresión que nos da la velocidad del murciélago obtenemos
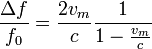
Si vm = 5 m/s y c = 343 m/s tenemos 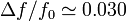 . Por tanto está justificado
utilizar las expresiones aproximadas.
. Por tanto está justificado
utilizar las expresiones aproximadas.






