Partícula en un tubo con muelle

De Laplace

(Diferencias entre revisiones)

Revisión de 21:32 22 feb 2010

Contenido

1 Enunciado
2 Ecuaciones de movimiento
- 2.1 En el sistema móvil
- 2.2 En el sistema fijo

1 Enunciado

Un tubo delgado, hueco y de masa despreciable, está situado en el plano horizontal $O X Y$ pudiendo rotar libremente y sin rozamiento alrededor del eje fijo (eje $O Z$ ) que pasa por su punto medio (punto O). En el interior del tubo se halla una partícula $P$ , de masa $m$ , que es atraída hacia el punto $O$ con una fuerza directamente proporcional a la distancia entre $P$ y $O$ (con constante de proporcionalidad $k$ ) Suponiendo que todos los contactos son lisos, y utilizando las coordenadas polares \rho y \theta, así como sus derivadas temporales de primer y segundo orden, se pide:

Escribir las ecuaciones dinámicas de la partíıcula (Segunda Ley de Newton proyectada en las direcciones radial y acimutal) en el sistema inercial $O X Y$ y en el sistema no inercial solidario con el tubo.
Se hace rotar el tubo con velocidad angular constante $ω 0$ . Determina que inecuación debe verificar \omega_0 respecto a m y k para que el movimiento de la partícula respecto al tubo pueda ser armónico simple.

2 Ecuaciones de movimiento

2.1 En el sistema móvil

En un sistema que gira con la barra, la partícula realiza un movimiento unidimensional, sometida a la acción del muelle y a las fuerzas de inercia. En forma vectorial tenemos, si la barra es el sólido “0” y la partícula es el sólido 2

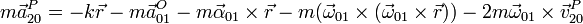
$m\vec{a}^P_{20} = -k\vec{r}-m\vec{a}^O_{01}-m\vec{\alpha}_{01}\times\vec{r}-m(\vec{\omega}_{01}\times(\vec{\omega}_{01}\times\vec{r}))-2m\vec{\omega}_{01}\times\vec{v}^P_{20}$

Veamos cada término de esta ecuación, proyectando sobre los ejes $X 0 Y 0 Z 0$

Fuerza elástica: Esta es la fuerza recuperadora que el resorte ejerce sobre la partícula. Si la distancia al centro es $ρ$ , esta fuerza vale

$\vec{F}=-k\vec{r}=-k\rho\vec{\imath}_0$

Fuerza de arrastre: Está asociada a la aceleración del origen del sistema de coordenadas, que en este caso está en reposo,

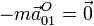
$-m\vec{a}^O_{01}=\vec{0}\,$

Término de aceleración angular: la aceleración angular del sistema de referencia es

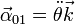
$\vec{\alpha}_{01}=\ddot{\theta}\vec{k}$

por lo que la fuerza de inercia debida a esta aceleración es

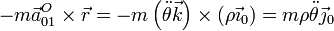
$-m\vec{a}^O_{01}\times\vec{r}=-m\left(\ddot{\theta}\vec{k}\right)\times(\rho \vec{\imath}_0)=m\rho\ddot{\theta}\vec{\jmath}_0$

Fuerza centrífuga: La velocidad angular del sistema de referencia es

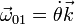
$\vec{\omega}_{01}=\dot{\theta}\vec{k}$

así que la fuerza centrífuga sobre la partícula es

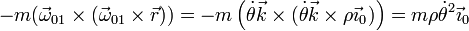
$-m(\vec{\omega}_{01}\times(\vec{\omega}_{01}\times\vec{r}))=-m\left(\dot{\theta}\vec{k}\times(\dot{\theta}\vec{k}\times\rho\vec{\imath}_0)\right)=m\rho\dot{\theta}^2\vec{\imath}_0$

2.2 En el sistema fijo

La segunda ley de Newton nos dice que

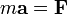
$m\mathbf{a}=\mathbf{F}\,$

siendo 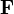$\mathbf{F}$ la resultante de las fuerzas sobre la partícula. Escribiendo la aceleración en coordenadas polares

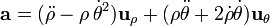
$\mathbf{a}=(\ddot{\rho}-\rho\,\dot{\theta}^2)\mathbf{u}_\rho+(\rho\ddot{\theta}+2\dot{\rho}\dot{\theta})\mathbf{u}_\theta$

nos queda

\

@@ Línea 28: / Línea 28: @@
 <center><math>-m\vec{a}^O_{01}\times\vec{r}=-m\left(\ddot{\theta}\vec{k}\right)\times(\rho \vec{\imath}_0)=m\rho\ddot{\theta}\vec{\jmath}_0</math></center>
+;Fuerza centrífuga: La velocidad angular del sistema de referencia es
+<center><math>\vec{\omega}_{01}=\dot{\theta}\vec{k}</math></center>
+:así que la fuerza centrífuga sobre la partícula es
+<center><math>-m(\vec{\omega}_{01}\times(\vec{\omega}_{01}\times\vec{r}))=-m\left(\dot{\theta}\vec{k}\times(\dot{\theta}\vec{k}\times\rho\vec{\imath}_0)\right)=m\rho\dot{\theta}^2\vec{\imath}_0</math></center>
 ===En el sistema fijo===

Partícula en un tubo con muelle

De Laplace

Revisión de 21:32 22 feb 2010

Contenido

1 Enunciado

2 Ecuaciones de movimiento

2.1 En el sistema móvil

2.2 En el sistema fijo

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES