Propulsión solar
De Laplace
(Diferencias entre revisiones)
(Nueva página: ==Introducción== ==Fundamentos== ===Partículas y cuadrivectores=== ===Fotones=== ===Transformaciones de Lorentz=== ===Efecto Doppler=== ==Colisiones relativistas== ===Entre dos part...) |
(→Partículas y cuadrivectores) |
||
| Línea 2: | Línea 2: | ||
==Fundamentos== | ==Fundamentos== | ||
===Partículas y cuadrivectores=== | ===Partículas y cuadrivectores=== | ||
| + | La cantidad de movimiento energía de una partícula puede describirse por el cuadrivector | ||
| + | |||
| + | <center><math>p^\mu=(\mathbf{p},E}</math></center> | ||
| + | |||
| + | donde la parte espacial es la cantidad de movimiento ordinaria, y la parte temporal es la energía de la partícula. El módulo de este cuadrivector es el cuadrado de la masa en reposo de la partícula. | ||
| + | |||
| + | <center><math>p^\mu p_\mu = E^2 - |\mathbf{p}|^2 = m^2</math></center> | ||
| + | |||
| + | En este problema, en que todo ocurre en una sola dimensión, la parte espacial se reduce a una sola componente | ||
| + | |||
| + | <center><math>p^\mu = (p,0,0,E)\,</math></center> | ||
| + | |||
| + | por lo que podemos prescindir de la segunda y la tercera y escribir simplemente | ||
| + | |||
| + | <center><math>p^\mu = (p,E)</math></center> | ||
| + | |||
| + | con el módulo | ||
| + | |||
| + | <center><math>p^\mu p_\mu = E^2-p^2 = m^2</math></center> | ||
| + | |||
===Fotones=== | ===Fotones=== | ||
===Transformaciones de Lorentz=== | ===Transformaciones de Lorentz=== | ||
Revisión de 20:01 19 feb 2010
Contenido |
1 Introducción
2 Fundamentos
2.1 Partículas y cuadrivectores
La cantidad de movimiento energía de una partícula puede describirse por el cuadrivector
donde la parte espacial es la cantidad de movimiento ordinaria, y la parte temporal es la energía de la partícula. El módulo de este cuadrivector es el cuadrado de la masa en reposo de la partícula.

En este problema, en que todo ocurre en una sola dimensión, la parte espacial se reduce a una sola componente
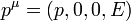
por lo que podemos prescindir de la segunda y la tercera y escribir simplemente
con el módulo





