Colisiones de dos partículas
De Laplace
(→Conservación de la cantidad de movimiento) |
(→Conservación de la cantidad de movimiento) |
||
| Línea 24: | Línea 24: | ||
Al ser la colisión el resultado de fuerzas internas, la cantidad de movimiento se conserva en todo momento. Por tanto, su valor inicial y su valor final deben ser iguales y | Al ser la colisión el resultado de fuerzas internas, la cantidad de movimiento se conserva en todo momento. Por tanto, su valor inicial y su valor final deben ser iguales y | ||
| - | <center><math>m_1v_1+m_2v_2 = m_1v'_1 + m_2v'_2</math></center> | + | <center><math>m_1v_1+m_2v_2 = m_1v'_1 + m_2v'_2\,</math></center> |
| + | |||
| + | Esta es la ecuación básica que gobierna las colisiones. | ||
==Conservación de la energía== | ==Conservación de la energía== | ||
Revisión de 20:54 19 feb 2010
Contenido |
1 Definición
Una colisión entre dos partículas es una interacción entre dos partículas que ocurre en un espacio limitado y un intervalo de tiempo corto.
Al considerar una colisión no nos interesa tanto el qué ocurre durante la colisión, sino la relación entre el estado de las partículas antes y después de la colisión. Para ello, lo que se utiliza es que las interacciones conservarán la cantidad de movimiento, el momento cinético y, en ciertas ocasiones, la energía cinética.
También es una colisión un péndulo balístico en el cual una bala se empotra en un objeto masivo, comunicándole una cierta velocidad. Aunque la interacción de la bala y el péndulo se puede considerar que continúa tras la colisión (pues ahora forman el mismo sólido), los cambios bruscos de velocidad se producen en un intervalo reducido de tiempo.
No es una colisión una interacción a grandes distancias o que se prolonga durante un periodo largo de tiempo. Por ejemplo, la atracción gravitatoria entre dos masas que orbitan la una alrededor de la otra es un estado permanente y no puede ser considerada una colisión.
El concepto de intervalo de tiempo corto o largo es relativo. La comparación se hace con el intervalo de tiempo en el que estamos considerando el movimiento de la partículas. Por ejemplo, cuando se lanza un satélite a Saturno, la nave se mueve por la atracción gravitatoria solar durante años, por lo que esta atracción no es una colisión. Sin embargo, durante el camino, para acelerar la nave, se puede emplear el método de catapulta gravitatoria, haciéndola pasar junto a Júpiter y ganando energía en el encuentro. Este acercamiento a Júpiter dura algunos días y sí puede ser tratado como una colisión (aunque la nave no llega a “tocar” Júpiter, sólo su campo gravitatorio).
2 Choques unidimensionales
La descripción de una colisión suele hacerse en dos sistemas de referencia diferentes, ambos inerciales. Uno es el llamado sistema laboratorio, que representa a un observador externo al sistema de dos partículas. El otro es el sistema centro de masas (CM), ligado al centro de masas del sistema de dos partículas. En el sistema CM la descipción es más sencilla, pero, dado que las medidas experimentales son realizadas en el sistema laboratorio, el procedimiento habitual es comenzar el estudio en el sistema laboratorio, pasar al sistema centro de masas, analizar la colisión en éste, y luego transformar los resultados de vuelta al sistema laboratorio.
Aquí, por simplicidad, consideraremos solo el choque de dos masas que, tras la colisión, se separan en la misma dirección en la que se acercaron. Esto permite usar cantidades escalares en lugar de vectores.
Suponemos entonces dos partículas, de masas m1 y m2 que se mueven con velocidades v1 y v2, respectivamente. Tras la colisión las velocidades pasarán a ser v'1 y v'2
Al ser un problema sencillo, puede prescindirse del sistema CM para determinar el resultado de la colisión.
3 Conservación de la cantidad de movimiento
Al ser la colisión el resultado de fuerzas internas, la cantidad de movimiento se conserva en todo momento. Por tanto, su valor inicial y su valor final deben ser iguales y
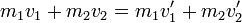
Esta es la ecuación básica que gobierna las colisiones.
