Teorema de conservación de la energía mecánica
De Laplace
(→Teorema de las fuerzas vivas) |
(→Fuerzas conservativas) |
||
| Línea 33: | Línea 33: | ||
El trabajo realizado por una fuerza cuando una partícula se mueve desde un punto A a un punto B depende en general del camino recorrido. Por ejemplo, una fuerza de rozamiento realiza un trabajo mayor cuanto mayor sea la distancia recorrida, aunque los puntos iniciales y finales sean los mismos en todos los caminos. | El trabajo realizado por una fuerza cuando una partícula se mueve desde un punto A a un punto B depende en general del camino recorrido. Por ejemplo, una fuerza de rozamiento realiza un trabajo mayor cuanto mayor sea la distancia recorrida, aunque los puntos iniciales y finales sean los mismos en todos los caminos. | ||
| - | Existe una clase de fuerzas, denominadas ''[[fuerzas conservativas]]'', para las cuales el trabajo entre dos puntos es independiente del camino que se emplea para ir de uno a otro | + | Existe una clase de fuerzas, denominadas ''[[Fuerza conservativa|fuerzas conservativas]]'', para las cuales el trabajo entre dos puntos es independiente del camino que se emplea para ir de uno a otro |
<center><math>W_{A\to B}=\int_{\!\!\!\!\!\!\!\!\!\!\!\! C_1\ A}^B \mathbf{F}\cdot\mathrm{d}\mathbf{r}=\int_{\!\!\!\!\!\!\!\!\!\!\!\! C_2\ A}^B \mathbf{F}\cdot\mathrm{d}\mathbf{r}</math></center> | <center><math>W_{A\to B}=\int_{\!\!\!\!\!\!\!\!\!\!\!\! C_1\ A}^B \mathbf{F}\cdot\mathrm{d}\mathbf{r}=\int_{\!\!\!\!\!\!\!\!\!\!\!\! C_2\ A}^B \mathbf{F}\cdot\mathrm{d}\mathbf{r}</math></center> | ||
| Línea 41: | Línea 41: | ||
<center><math>W_{A\to B}= \int_A^B \mathbf{F}\cdot\mathrm{d}\mathbf{r}</math></center> | <center><math>W_{A\to B}= \int_A^B \mathbf{F}\cdot\mathrm{d}\mathbf{r}</math></center> | ||
| - | donde la integral se calcula por un camino arbitrario | + | donde la integral se calcula por un camino arbitrario. |
Para el caso de fuerzas conservativas puede enunciarse un teorema complementario al [[teorema de las fuerzas vivas]]. | Para el caso de fuerzas conservativas puede enunciarse un teorema complementario al [[teorema de las fuerzas vivas]]. | ||
Revisión de 10:37 16 feb 2010
Contenido |
1 Teorema de las fuerzas vivas
El trabajo realizado sobre una partícula que se mueve desde un punto A a un punto B recorriendo una curva C es igual a la suma de los trabajos elementales a lo largo de dicha curva
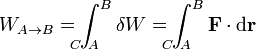
Se define asimismo la potencia desarrollada por la fuerza como el trabajo que realiza durante un tiempo dt, dividido por dicho intervalo
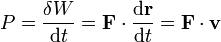
Aplicando la segunda ley de Newton la potencia desarrollada por una fuerza puede escribirse como la derivada respecto al tiempo de la energía cinética
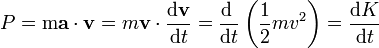
siendo K la energía cinética de la partícula
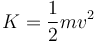
(donde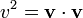 
es el módulo de la velocidad, o celeridad, al cuadrado).
Integrando respecto al tiempo obtenemos el teorema de las fuerzas vivas (o teorema trabajo-energía cinética):
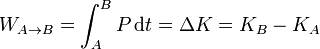
En palabras:
- “El trabajo realizado sobre una partícula entre dos puntos equivale al incremento de la energía cinética de dicha partícula.”
El trabajo realizado no tiene por qué ser necesariamente positivo. Si la partícula se ve frenada, su energía cinética disminuye y el trabajo resultante es negativo.
2 Fuerzas conservativas
El trabajo realizado por una fuerza cuando una partícula se mueve desde un punto A a un punto B depende en general del camino recorrido. Por ejemplo, una fuerza de rozamiento realiza un trabajo mayor cuanto mayor sea la distancia recorrida, aunque los puntos iniciales y finales sean los mismos en todos los caminos.
Existe una clase de fuerzas, denominadas fuerzas conservativas, para las cuales el trabajo entre dos puntos es independiente del camino que se emplea para ir de uno a otro
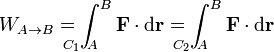
para una fuerza conservativa, por tanto, podemos omitir la indicación de la curva y escribir simplemente
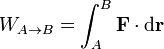
donde la integral se calcula por un camino arbitrario.
Para el caso de fuerzas conservativas puede enunciarse un teorema complementario al teorema de las fuerzas vivas.
Tenemos que el trabajo realizado por una fuerza conservativa en un desplazamiento de una partícula entre un punto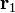 
y uno 
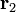es
Puesto que el camino para ir de un punto a otro es arbitrario, podemos tomar uno que pase por 
, el origen de potencial. De esta forma, podemos expresar el trabajo como diferencia entre dos energías potenciales
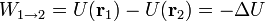
esto es:
- “El trabajo realizado por una fuerza conservativa es igual al decremento de su energía potencial.”
Combinando este teorema con el de las fuerzas vivas se llega al teorema de conservación de la energía mecánica.
3 Teorema de conservación de la energía mecánica
Cuando existe una energía potencial de la cual deriva la fuerza que actúa sobre una partícula se cumple la siguiente identidad
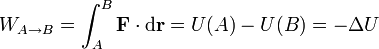
esto es, el trabajo realizado sobre la partícula es igual a la disminución de su energía potencial.
Combinando este teorema con el de las fuerzas vivas obtenemos
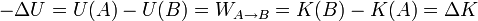
esto es, la que disminuye la energía potencial es igual a lo que aumenta la energía cinética (o viceversa). Reagrupando términos y definiendo la energía mecánica de la partícula como la suma de su energía cinética más la potencial obtenemos
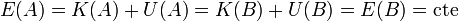
lo que se conoce como teorema de conservación de la energía mecánica:
- “En ausencia de fuerzas no conservativas, la energía mecánica de una partícula permanece constante.”
Este teorema deja de cumplirse cuando sobre la partícula actúan fuerzas no conservativas, como el rozamiento. Las fuerzas que reducen la energía mecánica (normalmente transformándola en calor) se conocen como fuerzas disipativas.
