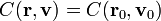Teoremas de conservación para una partícula
De Laplace
(→Constantes de movimiento) |
(→Constantes de movimiento) |
||
| Línea 2: | Línea 2: | ||
Una '''constante de movimiento''' o '''integral primera''' es una magnitud, de pendiente de la posición y velocidad de la partícula (o de las partículas, si hay más de una), cuyo valor no depende del tiempo, pese a que la posición y la velocidad si son variables en el tiempo | Una '''constante de movimiento''' o '''integral primera''' es una magnitud, de pendiente de la posición y velocidad de la partícula (o de las partículas, si hay más de una), cuyo valor no depende del tiempo, pese a que la posición y la velocidad si son variables en el tiempo | ||
| - | <center><math>C | + | <center><math>\frac{\mathrm{d}C}{\mathrm{d}t}(\mathbf{r},\mathbf{v})=0\quad\forall t</math>{{tose}}<math>C(\mathbf{r},\mathbf{v})=\mathrm{cte.}</math></center> |
El ejemplo más intuitivo, que veremos más adelante, es el de la energía mecánica. Cuando un cuerpo cae, su posición varía y su velocidad aumenta, pero la energía mecánica, que es una cierta combinación de la posición y la velocidad, permanece constante. | El ejemplo más intuitivo, que veremos más adelante, es el de la energía mecánica. Cuando un cuerpo cae, su posición varía y su velocidad aumenta, pero la energía mecánica, que es una cierta combinación de la posición y la velocidad, permanece constante. | ||
Revisión de 10:00 12 feb 2010
Contenido |
1 Constantes de movimiento
Una constante de movimiento o integral primera es una magnitud, de pendiente de la posición y velocidad de la partícula (o de las partículas, si hay más de una), cuyo valor no depende del tiempo, pese a que la posición y la velocidad si son variables en el tiempo
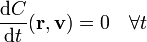

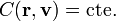
El ejemplo más intuitivo, que veremos más adelante, es el de la energía mecánica. Cuando un cuerpo cae, su posición varía y su velocidad aumenta, pero la energía mecánica, que es una cierta combinación de la posición y la velocidad, permanece constante.
Se denominan también ``integrales primeras, porque estas cantidades suelen obtenerse integrando una vez las ecuaciones de movimiento.
El hallazgo de una constante de movimiento en un problema simplifica la solución de éste, ya que permite establecer relaciones entre las variables y limita el número de soluciones posibles.
El valor concreto de una constante de movimiento puede calcularse a partir de las condiciones iniciales (o de los valores de la posicióin y velocidad en cualquier instante)