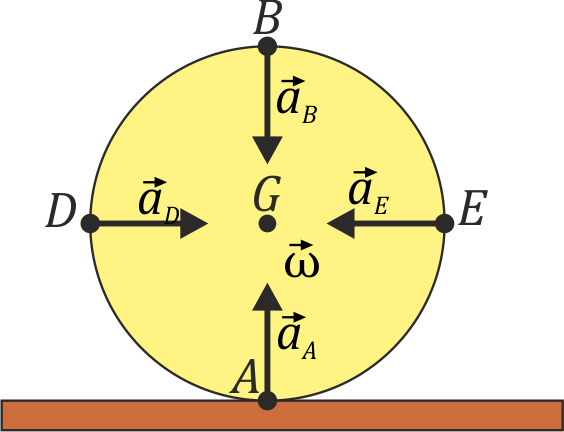
Velocidades y aceleraciones en un disco rodante sobre un plano
De Laplace
Contenido |
1 Enunciado
Un disco de radio R rueda sin deslizamiento sobre el plano horizontal y = 0 de forma que la posición de su centro sigue una ley
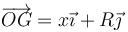
En función de x y sus derivadas temporales 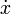 y
y 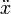 halle
halle
- La velocidad angular del disco.
- La velocidad del punto B situado diametralmente opuesto al de contacto con el suelo, A, así como de los puntos D y E situados en los extremos de un diámetro horizontal.
- La aceleración angular del disco
- Las aceleraciones de los puntos A, B, D y E.
2 Velocidad angular
La condición que define la rodadura sin deslizamiento es que en el punto de contacto con el suelo, A, la velocidad es nula en cada instante
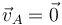
Por la expresión del campo de velocidades
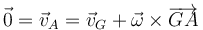
Por tratarse de un movimiento plano la velocidad angular es perpendicular al plano del movimiento
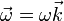
lo que da la condición
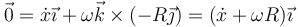
Por tanto
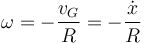
Hay que destacar que esta es una relación entre cantidades escalares, las componentes de los vectores. No una relación entre vectores, ya que la velocidad del centro y la angular llevan direcciones diferentes

El signo negativo indica que cuando el disco avanza su giro es en sentido horario.
3 Velocidad de otros puntos
Una vez que tenemos la velocidad del centro y la angular podemos hallar la velocidad de cualquier otro punto.
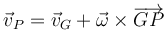
Alternativamente, dado que la velocidad de A es nula
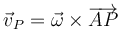
Así, para el punto B, situado en el extremo superior del disco
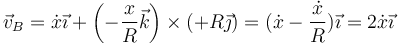
Vemos que resulta el doble de la velocidad del centro del disco. Esto es, si un vehículo avanza a 120 km/h, el extremo superior de sus ruedas va a 240 km/h.
Para el punto D situado en la parte trasera del disco respecto a la dirección de avance,
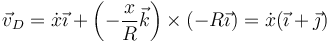
y para el punto D, situado en la delantera
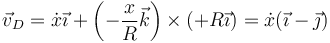
Todas esta velocidades cumplen que son tangentes a circunferencias con centro en A, centro instantáneo de rotación y perpendiculares al vector de posición relativa desde A.
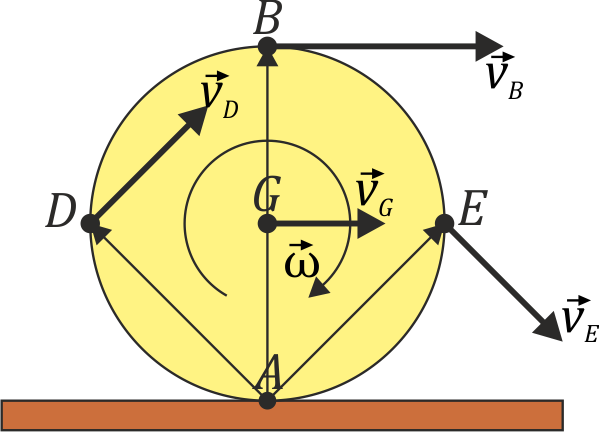
4 Aceleración angular
El movimiento de la rueda no tiene por qué ser uniforme, sino que su centro puede tener una aceleración
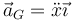
Si el disco rueda sin deslizar en todo instante, quiere decir que también tendrá una aceleración angular, ya que el aumento de la velocidad lineal implica un aumento de la angular.
Puesto que la relación
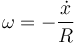
se cumple en cada instante y relaciona dos magnitudes medibles, la podemos derivar respecto al tiempo
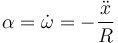
En forma vectorial
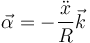
5 Aceleraciones de los diferentes puntos
la aceleración de cada punto la hallamos mediante la expresión del campo de aceleraciones
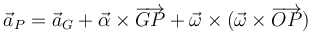
En el caso particular del movimiento plano tenemos que las posiciones y aceleraciones están siempre en el plano OXY mientras que la velocidad y la aceleración son ortogonales a este plano. Esto permite simplificar el doble producto vectorial y escribir
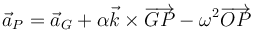
Para el punto A, de contacto con el suelo, la aceleración vale
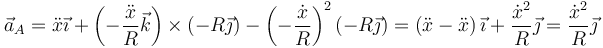
Los dos primeros términos se anulan entre sí, pero el tercero permanece.
Vemos que aunque la velocidad de A es nula en cada instante, su aceleración no es nula. ¿Cómo es posible? ¿Acaso la derivada de 0 no es 0? La respuesta es que el punto A es distinto en cada instante. A medido que la rueda avanza el punto material de la rueda que toca el suelo y el punto material del suelo que es tocado van cambiando. Por ello, no se puede derivar respecto al tiempo la velocidad instantánea de A para obtener su aceleración.
Si podemos derivar la velocidad de G, ya que este punto material sí es el mismo en todo instante. Como regla general, a la hora de analizar campos de aceleraciones hay que centrarse en puntos fijos o en articulaciones, que son puntos materiales cuya posición, velocidad y aceleración se conoce.
De manera similar obtenemos la aceleración del resto de puntos. Para B
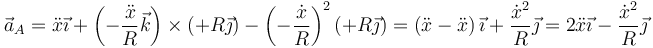
Para D
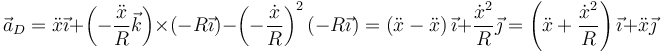
y para E
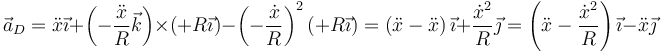
En el caso de que el centro de la rueda no esté acelerado (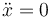 ) para los cuatro puntos resulta una aceleración normal dirigida hacia el centro de la circunferencia.
) para los cuatro puntos resulta una aceleración normal dirigida hacia el centro de la circunferencia.