Velocidad de escape (GIOI)

De Laplace

Contenido

1 Enunciado
2 Velocidad de escape
3 Caso terrestre, lunar y marciano
4 Escape del campo solar
5 Agujero negro clásico

1 Enunciado

Se define la velocidad de escape de un campo gravitatorio como aquella que permite llegar al infinito con velocidad nula. Sabiendo que la energía potencial gravitatoria tiene la expresión

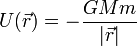
$U(\vec{r})=-\frac{GMm}{|\vec{r}|}$

Determine la velocidad de escape que debe tener un cuerpo para salir de la superficie terrestre hacia el espacio exterior.
Halle los valores numéricos para el caso de la superficie terrestre, la lunar y la marciana (consulte los datos de las masas en internet).
Calcule los valores de la velocidad de escape respecto al Sol para un cohete que se encuentre en la órbita terrestre.
Determine el radio que debería tener el Sol para que ni la luz pudiera escapar de él.

2 Velocidad de escape

La velocidad de escape se define como la mínima velocidad que es preciso comunicar a un cuerpo ligero para salir del campo gravitatorio de otro masivo.

Esta velocidad mínima es la que permite llegar al infinito con velocidad nula. Una velocidad menor no permitiría salir del “pozo” de energía potencial gravitatoria.

La energía mecánica de una partícula en un campo gravitatorio es

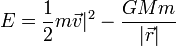
$E = \frac{1}{2}m\vec{v}|^2 - \frac{GMm}{|\vec{r}|}$

Imponiendo que 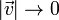$|\vec{v}|\to 0$ cuando 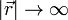$|\vec{r}|\to\infty$ queda

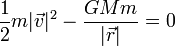
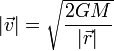
$\frac{1}{2}m|\vec{v}|^2-\frac{GMm}{|\vec{r}|}=0$ $\Rightarrow$ $|\vec{v}| = \sqrt{\frac{2GM}{|\vec{r}|}}$

Aquí $r$ es la distancia de partida, que usualmente será igual al radio del planeta

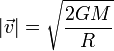
$|\vec{v}| = \sqrt{\frac{2GM}{R}}$

3 Caso terrestre, lunar y marciano

El valor del producto GM es conocido con mayor precisión que el valor de la constante de gravitación universal y que la masa de cada planeta por separado. El radio medio de la Tierra, Luna y Marte también es conocido con precisión. El radio del Sol es más incierto, por tratarse de una esfera gaseosa. Así tenemos

Cuerpo	GM (km³/s²)	R (km)
Tierra	398 600.4418	6 370
Luna	4 902.7779	1 737
Marte	42 828	3 386
Sol	132 712 440 018	695 500

Esto da las siguientes velocidades de escape:

Tierra

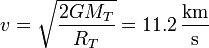
$v = \sqrt{\frac{2GM_T}{R_T}}=11.2\,\frac{\mathrm{km}}{\mathrm{s}}$

Luna

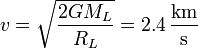
$v = \sqrt{\frac{2GM_L}{R_L}}=2.4\,\frac{\mathrm{km}}{\mathrm{s}}$

Marte

$v = \sqrt{\frac{2GM_M}{R_M}}=5.0\,\frac{\mathrm{km}}{\mathrm{s}}$

4 Escape del campo solar

Con una velocidad de 11.2 km/s un cohete puede escapar de la atracción terrestre, pero ello no quiere decir que pueda escapar del Sistema Solar, pues no solo debe vencer la atracción terrestre sino también la que produce el Sol.

A una distancia del Sol igual al radio de la órbita terrestre (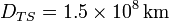 $D_{TS} = 1.5\times 10^8\,\mathrm{km}$ ) la velocidad de escape del campo solar es

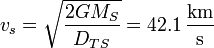
$v_s= \sqrt{\frac{2GM_S}{D_{TS}}}= 42.1\,\frac{\mathrm{km}}{\mathrm{s}}$

que es muy superior a la terrestre.

la velocidad con la que debería ser disparado el cohete desde la superficie terrestre para sacarlo del Sistema Solar no es la suma de las dos velocidades de escape, sino aquella que hace que la rapidez en el infinito (respecto de la Tierra) es igual a la velocidad de escape del Sol, es decir

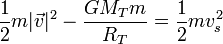
$\frac{1}{2}m|\vec{v}|^2-\frac{GM_Tm}{R_T}=\frac{1}{2}mv_s^2$

lo que da la velocidad de lanzamiento

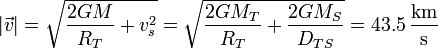
$|\vec{v}| = \sqrt{\frac{2GM}{R_T}+v_s^2}=\sqrt{\frac{2GM_T}{R_T}+\frac{2GM_S}{D_{TS}}}= 43.5\,\frac{\mathrm{km}}{\mathrm{s}}$

Esta velocidad es tan gigantesca que para conseguir sacar un satélite del Sistema Solar (como las sondas Pioneer o Voyager) se emplean otros métodos de impulso, como la catapulta gravitatoria.

5 Agujero negro clásico

Un problema relacionado es el de determinar qué radio debe tener una estrella como el Sol si queremos que ni la luz pueda escapar de su superficie. Para ello, la velocidad de escape debe ser igual a $c$ , la velocidad de la luz. Esto da el radio

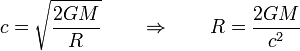
$c = \sqrt{\frac{2GM}{R}}\qquad\Rightarrow\qquad R = \frac{2GM}{c^2}$

que para el caso del Sol da

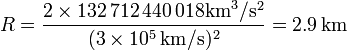
$R = \frac{2\times 132\,712\,440\,018\mathrm{km}^3/\mathrm{s}^2}{(3\times 10^5\,\mathrm{km}/\mathrm{s})^2} = 2.9\,\mathrm{km}$

esto es, el Sol debería encogerse a media cienmilésima de su radio (y su densidad multiplicarse por un factor de $1016$ ), para que se convirtiera en lo que se denomina un agujero negro clásico, del cual la luz no podría escapar sino que volvería a caer sobre la superficie de la estrella. Este concepto fue introducido por Michell y Laplace en el siglo XVIII, y está relacionado pero no es lo mismo que el actual concepto de agujero negro, el cual requiere la teoría de la relatividad de Einstein.

Velocidad de escape (GIOI)

De Laplace

Contenido

1 Enunciado

2 Velocidad de escape

3 Caso terrestre, lunar y marciano

4 Escape del campo solar

5 Agujero negro clásico

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES