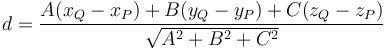Vectores en física. Coordenadas y componentes
De Laplace
Contenido |
1 Elementos geométricos
1.1 Puntos del espacio
En el espacio tridimensional, podemos etiquetar cada punto del espacio, empleando sistemas de coordenadas, o bien, dándoles nombres (A, B, C,...)
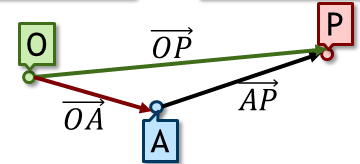
Dados dos puntos del espacio, definimos el vector de posición relativa de P respecto a A como que el que va de A a P, 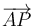 .
.
Dados tres puntos del espacio, podemos establecer una relación entre sus posiciones relativas
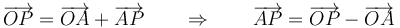
1.2 Ecuación vectorial de un plano
Un plano queda definido por uno de sus puntos, A, y un vector normal a él, 
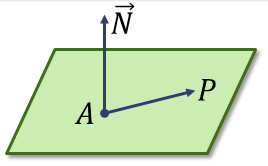
Dado cualquier otro punto del plano, P, se cumple que, el vector que lo une a A es perpendicular al vector normal.
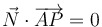
Esta es la ecuación vectorial del plano. Si lo que conocemos son las posiciones respecto a un punto dado O, queda
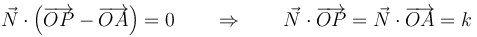
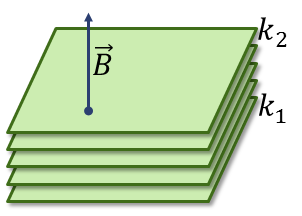
La última expresión es una constante en el sentido de que no depende del punto P del plano, sino solo de A (que ya era conocido) y del vector normal. Variando el valor de k obtenemos una serie de planos paralelos
Si lo que nos dan son tres puntos del plano, A, B, y C, el cálculo es similar sin más que calcular previamente el vector normal
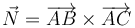
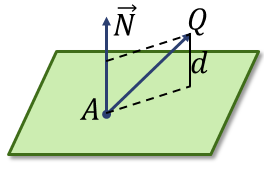
Si tenemos un punto Q exterior al plano, podemos hallar la distancia a éste (con signo) mediante la proyección ortogonal sobre el vector normal
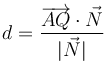
1.3 Ecuación vectorial de una recta
Una recta en el espacio queda definida por uno de sus puntos A, y un vector director  , de forma que cualquier otro punto de la recta queda definido por que
, de forma que cualquier otro punto de la recta queda definido por que
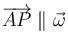
Esta relación de paralelismo puede expresarse diciendo que uno de los vectores es proporcional al otro

o que, al ser paralelos, su producto vectorial es nulo
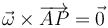
A esta última ecuación se la conoce como ecuación vectorial de la recta.
Si lo que conocemos son las posiciones respecto a un punto fijo O, estas ecuaciones quedan
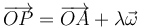
y
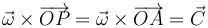
siendo  un cierto vector ortogonal a
un cierto vector ortogonal a  conocido, que es constante en el sentido de que no depende del punto P de la recta que estemos considerando.
conocido, que es constante en el sentido de que no depende del punto P de la recta que estemos considerando.
Si tenemos un punto Q exterior a la recta, podemos hallar la distancia a ésta con ayuda del producto vectorial
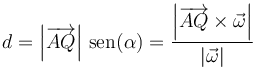
2 Momento de un vector respecto a un punto
Una de las operaciones vectoriales con más utilidad en física es el cálculo del momento de un vector respecto a un punto. Sea  un vector aplicado en un punto A y sea O otro punto del espacio. Se define el momento del vector
un vector aplicado en un punto A y sea O otro punto del espacio. Se define el momento del vector  respecto al punto O como el producto vectorial
respecto al punto O como el producto vectorial
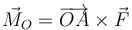
Este vector ligado al punto O posee las siguientes propiedades:
- Es ortogonal al vector
 , sea cual sea el punto O
, sea cual sea el punto O
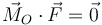
- Es ortogonal al plano definido por O y la recta soporte de
 (la que pasa por A y lleva la dirección de
(la que pasa por A y lleva la dirección de  ).
).
- Tiene un sentido que depende de a qué lado de la recta soporte se encuentra O dentro de dicho plano. A un lado apunto hacia afuera del plano y al otro hacia adentro, según la regla de la mano derecha.
- Su módulo es igual al producto
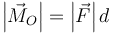
- siendo d la distancia de O a la recta soporte, de acuerdo con lo afirmado en la sección anterior.
- Si el vector
 en lugar de estar aplicado en A lo está en cualquier otro, B, de la misma recta soporte, el momento respecto a O es el mismo.
en lugar de estar aplicado en A lo está en cualquier otro, B, de la misma recta soporte, el momento respecto a O es el mismo.
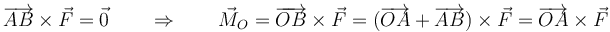
- El momento respecto a otro punto P se puede calcular conocidos el momento respecto a un punto O y el vector
 , aunque no se conozca el punto de aplicación A:
, aunque no se conozca el punto de aplicación A:
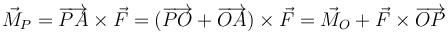
- En particular si el momento respecto al punto O es igual al momento respecto a P, los dos puntos se encuentran sobre una recta paralela a la recta soporte
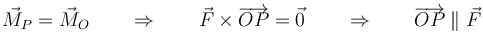
3 Sistemas de referencia
3.1 Definición
Los puntos del espacio pueden etiquetarse mediante letras, O, P, Q,… Sin embargo, para operar con ellos, es conveniente emplear coordenadas, que no son más que etiquetas numéricas que identifican cada punto de forma unívoca.
Existen muchos sistemas de coordenadas posibles. Las más sencillas son las coordenadas cartesianas
Dado un punto del espacio, O, que tomamos como origen de coordenadas, tomamos tres planos que pasan por dicho punto y que sean ortogonales entre sí, que denominaremos XY, XZ e YZ. Definimos entonces las coordenadas cartesianas de cualquier otro punto como las distancias (con signo), x, y, z a estos planos coordenados (x la distancia al YZ, y al XZ, y z al XY).
Los planos se cortan en tres rectas, también ortogonales entre sí, que denominamos ejes de coordenadas OX, OY y OZ (o simplemente X, Y y Z).
Los vectores unitarios tangentes a estos ejes forman una base ortonormal que denotamos como  .
.
Por ser ortonormales, verifican
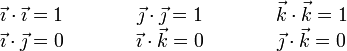
o, en forma de tabla:

| 
| 
| 
|
|---|---|---|---|

| 1 | 0 | 0 |

| 0 | 1 | 0 |

| 0 | 0 | 1 |
Esta base canónica es además dextrógira, esto es, verifica la regla de la mano derecha cuando los vectores se colocan en el orden  . Empleando el producto vectorial, esto se expresa
. Empleando el producto vectorial, esto se expresa
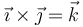
y análogamente para el resto de productos: positivo si se gira en sentido antihorario y negativo si se va en sentido horario en la figura. En forma de tabla:
| 
| 
| 
|
|---|---|---|---|

| 
| 
| 
|

| 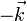
| 
| 
|

| 
| 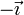
| 
|
3.2 Componentes de un vector
Una vez definida la base canónica, todo vector libre o ligado puede descomponerse de forma única en una parte paralela a  , una paralela a
, una paralela a  y otra paralela a
y otra paralela a 
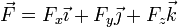
Donde cada una de las componentes Fx, Fy y Fz puede hallarse, según hemos visto, con ayuda del producto escalar
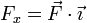
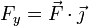
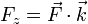
En Física es habitual trabajar simultáneamente con más de un sistema de referencia (por ejemplo, al describir del movimiento de un observador respecto a otro). Puesto que las componentes de un vector dependen de la base que se emplee para describirlo, es importante escribir los vectores como en la expresión anterior y NO en la forma 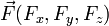 , ya que en esta última forma se pierde la información sobre la base en que se trabaja. La única excepción la constituye el vector de posición de un punto del espacio.
, ya que en esta última forma se pierde la información sobre la base en que se trabaja. La única excepción la constituye el vector de posición de un punto del espacio.
3.3 Vector de posición
La posición de cualquier punto P puede expresarse mediante su vector de posición, que es aquél que tiene como origen el de coordenadas y como extremo el punto P (es, por tanto, un vector ligado)
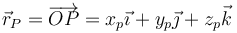
La posición del origen de coordenadas y la orientación de los ejes son arbitrarias. Por ello no hay que presuponer que, por ejemplo, “el eje Z es vertical”. Nadie se encuentra un eje Z por la calle. El eje Z será el que nosotros queramos que sea y si nos interesa que forme un ángulo de 37° respecto al suelo, pues así lo podemos tomar.
En forma abreviada, la posición del punto P se puede escribir en la forma P(xp,yp,zp)
La posición relativa del punto Q respecto al punto P la da el vector que tiene por origen P y por extremo Q. Es inmediato obtener las componentes de este vector en la base cartesiana, conocidas las coordenadas cartesianas del origen y del extremo. Basta restarle las primeras a las segundas. Si P(xp,yp,zp) y Q(xq,yq,zq), el vector 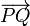 es:
es:
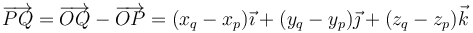
3.4 Expresión de las operaciones
3.4.1 Igualdad entre vectores
Dos vectores libres son equivalentes cuando tienen el mismo módulo, dirección y sentido. En términos de las componentes, dos vectores son equivalentes cuando son iguales componente a componente
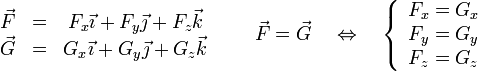
En particular, un vector es nulo si y solo si son nulas cada una de sus componentes.
3.4.2 Suma de vectores
Para sumar dos vectores, basta con sumar las componentes respectivas
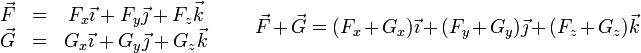
A la hora de sumar, hay que tener cuidado con sumar las componentes correspondientes al mismo vector de la base y tener en cuenta que alguna componente puede ser nula. Por ejemplo
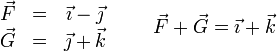
3.4.3 Producto por un escalar
Las componentes del producto de un vector por un escalar se obtienen multiplicando todas y cada una de ellas, por el escalar.
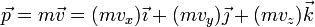
3.4.4 Producto escalar
El producto escalar se halla desarrollando la expresión
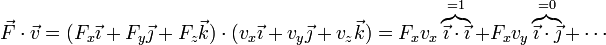
Como consecuencia de la ortonormalidad de la base, la expresión se reduce a
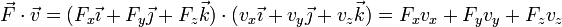
Conviene recordar que los productos son entre componentes correspondientes no “la primera por la primera más…” ya que es posible que alguna de ellas sea nula. Por ejemplo:
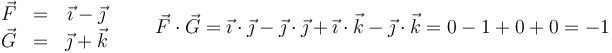
o bien
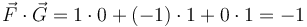
A partir del producto escalar se obtiene la expresión para el módulo de un vector en función de sus componentes cartesianas
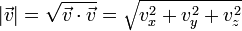
También permite determinar las componentes de un vector si éstas no se conocen previamente
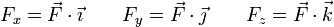
Por ejemplo, si se nos dice que una fuerza tiene de módulo 10 N y forma un ángulo de 60° con la vertical, tendremos que la componente vertical de la fuerza vale
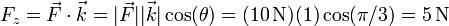
3.4.5 Producto vectorial
Las componentes del producto vectorial se hallan de manera análoga a las del producto escalar. Desarrollando la expresión correspondiente y en este caso sobreviven 6 términos de los 9
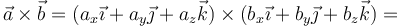
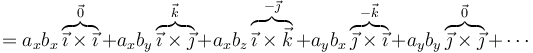
Si aquí agrupamos los coeficientes del mismo vector queda
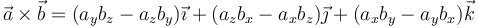
que se puede abreviar de manera simbólica como un determinante
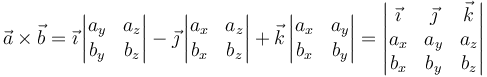
Así, por ejemplo, para
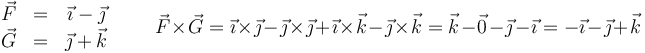
o, empleando el determinante
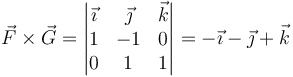
3.4.6 Producto mixto
Si combinamos las expresiones para el producto escalar y el vectorial queda una expresión sencilla para el producto mixto:
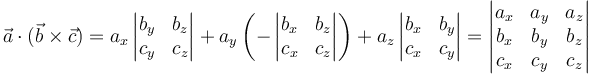
4 Ecuaciones de planos y rectas
4.1 De un plano
La ecuación vectorial de un plano
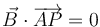
se desarrolla en términos de los vectores de posición como
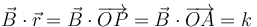
lo que equivale a escribir
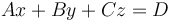
siendo
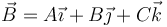
el vector normal al plano y D = k.
4.2 De una recta
La ecuación vectorial de la recta
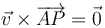
equivale a
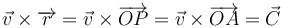
Al desarrollar por componentes resultan tres ecuaciones, pero de las que solo dos son independientes. Estas dos ecuaciones tienen la forma general
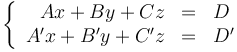
que equivale a decir que una recta es la intereseccion de dos planos, cumpliendo los respectivos vectores normales
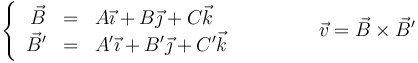
5 Distancias
5.1 Entre dos puntos
Si tenemos dos puntos P y Q, la distancia entre ellos es el módulo de su vector de posición relativo
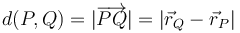
A su vez el módulo de un vector se puede hallar a partir del producto escalar del vector por sí mismo
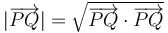
y usando la expresión del producto escalar en coordenadas cartesianas nos queda
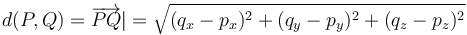
5.2 De un punto a una recta
De acuerdo con la ecuación anterior para la distancia de un punto O a una recta que pasa por A y lleva la dirección marcada por 
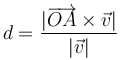
Es decir, basta con tomar un punto cualquiera de la recta (no tiene por qué ser el que está en la perpendicular) y hallar el vector de posición relativo respecto a O. Su producto vectorial por el vector director de la recta (dividido por el módulo de éste) nos da la distancia de Q a la recta en cuestión.
5.3 De un punto a un plano
Si tenemos un plano que pasa por el punto P y es ortogonal al vector  , la distancia de un punto Q al plano la da la ecuación
, la distancia de un punto Q al plano la da la ecuación
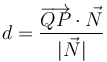
Esta cantidad tiene un signo que indica a que lado del plano se encuentra el punto. La distancia real sería el valor absoluto de ésta.
Si el vector  tiene las expresión
tiene las expresión
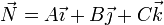
esta distancia con signo queda como