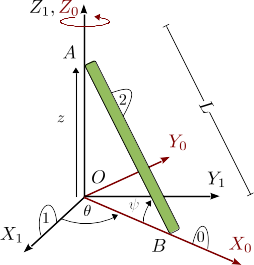
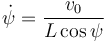Varilla rotando con extremo deslizando sobre un eje
De Laplace
Contenido |
1 Enunciado
El extremo A de una barra de longitud L desliza sobre el eje OZ1. La barra gira respecto al eje OZ1, de modo que está siempre contenida en el plano OX0Z0 y el punto B permanece siempre en el eje OX0. El plano OX0Z0 realiza una rotación de eje permanente OZ0. En el instante inicial el punto A coincidía con O y el punto B estaba sobre el eje OX1.
- Determina las reducciones cinemáticas de los movimientos {01}, {20} y {21}, así como sus derivadas. El resultado debe quedar en función de z, ψ, θ y sus derivadas temporales.
- Supongamos que la velocidad del punto A respecto al eje es constante y de magnitud v0. Encuentra la ecuación diferencial que determina la función ψ(t).
2 Solución
2.1 Reducciones cinemáticas
2.1.1 Movimiento {01}
Este movimiento es la rotación de eje permanente del plano OX0Z0 alrededor del eje OZ0. Todos los puntos del eje están en reposo en este movimiento, en particular el punto A. Entonces una posible reducción cinemática es
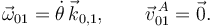
El eje del movimiento es 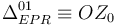 . Es una rotación permanente, porque el eje no cambia respecto al sólido "1". La derivada de la reducción cinemática es
. Es una rotación permanente, porque el eje no cambia respecto al sólido "1". La derivada de la reducción cinemática es

Hemos usado que 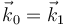 , y por tanto es constante visto desde el sólido "1".
, y por tanto es constante visto desde el sólido "1".
2.1.2 Movimiento {20}
El punto A de la barra (sólido "2"), se mueve respecto al eje OZ0, es decir, respecto al sólido "0". Entonces
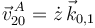
Por otro lado, este movimiento es una rotación plana de la barra en el plano OX0Z0. Entonces  es perpendicular a este plano. Observando el dibujo vemos que
es perpendicular a este plano. Observando el dibujo vemos que
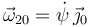
Cuando ψ aumenta, se tiene 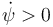 y esta expresión da el sentido correcto del vector rotación.
y esta expresión da el sentido correcto del vector rotación.
Este movimiento es una rotación pura, pues 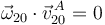 . La aceleración angular es
. La aceleración angular es
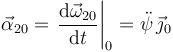
Hemos usado que el vector  está expresado en la base del sólido "0", por lo que el vector
está expresado en la base del sólido "0", por lo que el vector 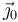 es constante en esta derivada.
Para la aceleración del punto A tenemos
es constante en esta derivada.
Para la aceleración del punto A tenemos
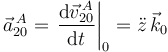
2.1.3 Movimiento {21}
Utilizamos la composición
{21} = {20} + {01}
Para el vector rotación
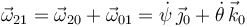
Para la velocidad en A
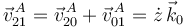
El vector aceleración angular
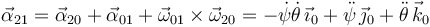
Y la aceleración en A
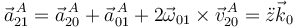
Este movimiento es helicoidal tangente, pues 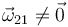 y
y 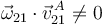 .
.
2.2 Ecuación para ψ
En estas condiciones tenemos
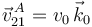
El punto B está obligado a moverse en el plano OX1Y1. Entonces su velocidad 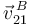 no tiene componente en Z0. Usando el Teorema de Chasles
no tiene componente en Z0. Usando el Teorema de Chasles
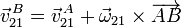
El vector 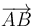 es
es
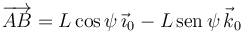
Por tanto
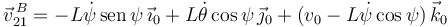
Como la componente en Z0 tiene que ser nula, obtenemos