Tres hilos en paralelo y en serie

De Laplace

Contenido

1 Enunciado
2 Intensidades de corriente
3 Potencia por efecto Joule
- 3.1 Antes de abrir los interruptores
- 3.2 Con los interruptores abiertos
4 Campo magnético
- 4.1 Antes de abrir los interruptores
  - 4.1.1 Punto P
  - 4.1.2 Punto Q
- 4.2 Con los interruptores abiertos
  - 4.2.1 Punto P
  - 4.2.2 Punto Q

1 Enunciado

Se tiene un sistema formado por tres hilos de constantán, una aleación que tiene conductividad 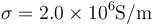$\sigma=2.0\times 10^6 \mathrm{S}/\mathrm{m}$ , los tres hilos son de la misma longitud, 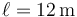$\ell=12\,\mathrm{m}$ . El hilo “1” tiene una sección transversal 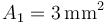$A_1=3\,\mathrm{mm}^2$ , el “2” una sección 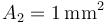$A_2=1\,\mathrm{mm}^2$ y el “3” una sección 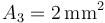$A_3=2\,\mathrm{mm}^2$ . Se disponen paralelamente, con una distancia entre ellos 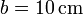$b=10\,\mathrm{cm}$ . Se conectan como indica la figura, con los interruptores A y B cerrados. Tanto los interruptores como las demás conexiones son ideales, sin resistencia. El hilo “1” se conecta a una fuente de tensión continua 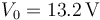$V_0=13.2\,\mathrm{V}$ y el “3” a tierra.

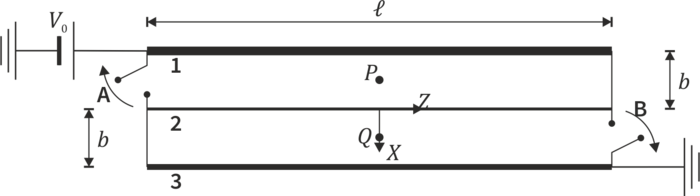
Se trata de comparar el estado de corriente continua antes de que se abran los interruptores y el estado de corriente continua después de abrir ambos.

Calcule la intensidad de corriente que circula por cada uno de los hilos.
1. Con los dos interruptores cerrados.
2. Con los dos interruptores abiertos.
Calcule la potencia consumida por efecto Joule en cada uno de los hilos y la total del sistema
1. Con los dos interruptores cerrados.
2. Con los dos interruptores abiertos.
Halle el campo magnético en los puntos P y Q, situados en los puntos medios entre los hilos “1” y “2”, y entre “2” y “3”.
1. Con los dos interruptores cerrados.
2. Con los dos interruptores abiertos.

2 Intensidades de corriente

2.1 Resistencias

Cada uno de los cables se comporta, desde el punto de vista del circuito, como un resistor, siendo las resistencias respectivas:

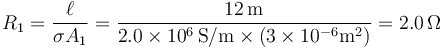
$R_1=\frac{\ell}{\sigma A_1}=\frac{12\,\mathrm{m}}{2.0\times 10^6\,\mathrm{S}/\mathrm{m}\times(3\times 10^{-6}\mathrm{m}^2)}=2.0\,\Omega$

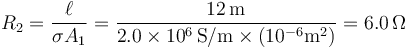
$R_2=\frac{\ell}{\sigma A_1}=\frac{12\,\mathrm{m}}{2.0\times 10^6\,\mathrm{S}/\mathrm{m}\times(10^{-6}\mathrm{m}^2)}=6.0\,\Omega$

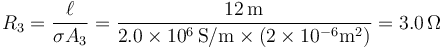
$R_3=\frac{\ell}{\sigma A_3}=\frac{12\,\mathrm{m}}{2.0\times 10^6\,\mathrm{S}/\mathrm{m}\times(2\times 10^{-6}\mathrm{m}^2)}=3.0\,\Omega$

2.2 Antes de abrir los interruptores

Antes de abrir los interruptores, las tres resistencias están en paralelo, por lo que la diferencia de potencial es la misma en cada uno de los cables. La ley de Ohm nos da la intensidad que circula por cada uno

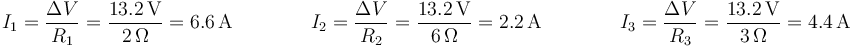
$I_1=\frac{\Delta V}{R_1}=\frac{13.2\,\mathrm{V}}{2\,\Omega}=6.6\,\mathrm{A} \qquad\qquad I_2=\frac{\Delta V}{R_2}=\frac{13.2\,\mathrm{V}}{6\,\Omega}=2.2\,\mathrm{A}\qquad\qquad I_3=\frac{\Delta V}{R_3}=\frac{13.2\,\mathrm{V}}{3\,\Omega}=4.4\,\mathrm{A}$

2.3 Con los interruptores abiertos

Una vez abiertos, los tres cables pasan a estar en serie. La intensidad de corriente va por el “1”, vuelve por el “2” y vuelve a avanzar por el “3”. La intensidad que circula por los tres la obtenemos de la ley de Ohm empleando la resistencia equivalente

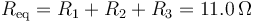
$R_\mathrm{eq}=R_1+R_2+R_3=11.0\,\Omega$

y resulta la intensidad de corriente

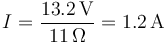
$I=\frac{13.2\,\mathrm{V}}{11\,\Omega}=1.2\,\mathrm{A}$

Si consideramos positivas las intensidades que van en el sentido del eje OZ y negativas las opuestas, queda

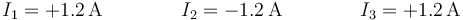
$I_1=+1.2\,\mathrm{A}\qquad\qquad I_2=-1.2\,\mathrm{A}\qquad\qquad I_3=+1.2\,\mathrm{A}$

3 Potencia por efecto Joule

3.1 Antes de abrir los interruptores

La potencia consumida por efecto Joule en cada cable nos la da la ley de Joule

$P=I^2R\,$

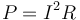
lo que nos da las potencias

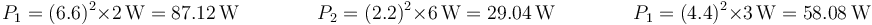
$P_1=(6.6)^2\times 2\,\mathrm{W}=87.12\,\mathrm{W}\qquad\qquad P_2=(2.2)^2\times 6\,\mathrm{W}=29.04\,\mathrm{W}\qquad\qquad P_1=(4.4)^2\times 3\,\mathrm{W}=58.08\,\mathrm{W}$

siendo la potencia total disipada

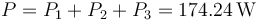
$P=P_1+P_2+P_3=174.24\,\mathrm{W}$

3.2 Con los interruptores abiertos

Operando de la misma manera

$P_1=(1.2)^2\times 2\,\mathrm{W}=2.88\,\mathrm{W}\qquad\qquad P_2=(1.2)^2\times 6\,\mathrm{W}=8.64\,\mathrm{W}\qquad\qquad P_1=(1.2)^2\times 3\,\mathrm{W}=4.32\,\mathrm{W}$

siendo ahora la potencia total

$P=P_1+P_2+P_3=15.84\,\mathrm{W}$

4 Campo magnético

4.1 Antes de abrir los interruptores

El campo magnético se calcula aplicando en cada caso la expresión para un hilo infinito (ya que 12m es mucho mayor que 10cm)

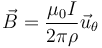
$\vec{B}=\frac{\mu_0 I}{2\pi\rho}\vec{u}_\theta$

4.1.1 Punto P

Tenemos para el primer hilo

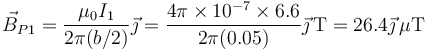
$\vec{B}_{P1}=\frac{\mu_0 I_1}{2\pi(b/2)}\vec{\jmath}=\frac{4\pi\times 10^{-7}\times 6.6}{2\pi(0.05)}\vec{\jmath}\,\mathrm{T}=26.4\vec{\jmath}\,\mu\mathrm{T}$

Para el segundo

$\vec{B}_{P2}=\frac{\mu_0 I_2}{2\pi(b/2)}\vec{\jmath}=\frac{4\pi\times 10^{-7}\times 2.2}{2\pi(0.05)}(-\vec{\jmath})\,\mathrm{T}=-8.8\vec{\jmath}\,\mu\mathrm{T}$

y para el tercero

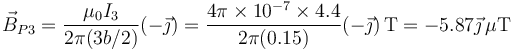
$\vec{B}_{P3}=\frac{\mu_0 I_3}{2\pi(3b/2)}(-\vec{\jmath})=\frac{4\pi\times 10^{-7}\times 4.4}{2\pi(0.15)}(-\vec{\jmath})\,\mathrm{T}=-5.87\vec{\jmath}\,\mu\mathrm{T}$

siendo el campo magnético en este punto

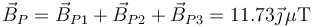
$\vec{B}_P=\vec{B}_{P1}+\vec{B}_{P2}+\vec{B}_{P3}=11.73\vec{\jmath}\,\mu\mathrm{T}$

En cada caso la dirección del vector $\vec{u}_\theta$ es del eje OY, pero su sentido depende de si estamos a un lado o al otro del hilo, según la regla de la mano derecha.

4.1.2 Punto Q

Para el primer hilo

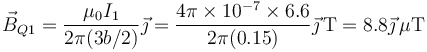
$\vec{B}_{Q1}=\frac{\mu_0 I_1}{2\pi(3b/2)}\vec{\jmath}=\frac{4\pi\times 10^{-7}\times 6.6}{2\pi(0.15)}\vec{\jmath}\,\mathrm{T}=8.8\vec{\jmath}\,\mu\mathrm{T}$

Para el segundo

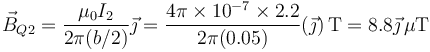
$\vec{B}_{Q2}=\frac{\mu_0 I_2}{2\pi(b/2)}\vec{\jmath}=\frac{4\pi\times 10^{-7}\times 2.2}{2\pi(0.05)}(\vec{\jmath})\,\mathrm{T}=8.8\vec{\jmath}\,\mu\mathrm{T}$

y para el tercero

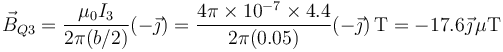
$\vec{B}_{Q3}=\frac{\mu_0 I_3}{2\pi(b/2)}(-\vec{\jmath})=\frac{4\pi\times 10^{-7}\times 4.4}{2\pi(0.05)}(-\vec{\jmath})\,\mathrm{T}=-17.6\vec{\jmath}\,\mu\mathrm{T}$

siendo el campo magnético en este punto

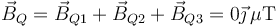
$\vec{B}_Q=\vec{B}_{Q1}+\vec{B}_{Q2}+\vec{B}_{Q3}=0\vec{\jmath}\,\mu\mathrm{T}$

4.2 Con los interruptores abiertos

Operamos de la misma manera teniendo cuidado de que ahora $I 2$ es negativa.

4.2.1 Punto P

Tenemos para el primer hilo

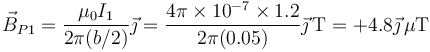
$\vec{B}_{P1}=\frac{\mu_0 I_1}{2\pi(b/2)}\vec{\jmath}=\frac{4\pi\times 10^{-7}\times 1.2}{2\pi(0.05)}\vec{\jmath}\,\mathrm{T}=+4.8\vec{\jmath}\,\mu\mathrm{T}$

Para el segundo

$\vec{B}_{P2}=\frac{\mu_0 I_2}{2\pi(b/2)}\vec{\jmath}=\frac{4\pi\times 10^{-7}\times (-1.2)}{2\pi(0.05)}(-\vec{\jmath})\,\mathrm{T}=+4.8\vec{\jmath}\,\mu\mathrm{T}$

y para el tercero

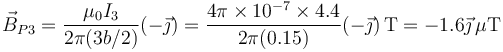
$\vec{B}_{P3}=\frac{\mu_0 I_3}{2\pi(3b/2)}(-\vec{\jmath})=\frac{4\pi\times 10^{-7}\times 4.4}{2\pi(0.15)}(-\vec{\jmath})\,\mathrm{T}=-1.6\vec{\jmath}\,\mu\mathrm{T}$

siendo el campo magnético en este punto

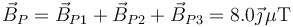
$\vec{B}_P=\vec{B}_{P1}+\vec{B}_{P2}+\vec{B}_{P3}=8.0\vec{\jmath}\,\mu\mathrm{T}$

4.2.2 Punto Q

Para el primer hilo

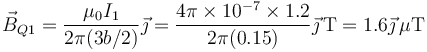
$\vec{B}_{Q1}=\frac{\mu_0 I_1}{2\pi(3b/2)}\vec{\jmath}=\frac{4\pi\times 10^{-7}\times 1.2}{2\pi(0.15)}\vec{\jmath}\,\mathrm{T}=1.6\vec{\jmath}\,\mu\mathrm{T}$

Para el segundo

$\vec{B}_{Q2}=\frac{\mu_0 I_2}{2\pi(b/2)}(-\vec{\jmath})=\frac{4\pi\times 10^{-7}\times (-1.2)}{2\pi(0.05)}(\vec{\jmath})\,\mathrm{T}=-4.8\vec{\jmath}\,\mu\mathrm{T}$

y para el tercero

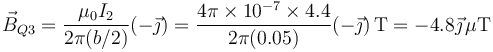
$\vec{B}_{Q3}=\frac{\mu_0 I_2}{2\pi(b/2)}(-\vec{\jmath})=\frac{4\pi\times 10^{-7}\times 4.4}{2\pi(0.05)}(-\vec{\jmath})\,\mathrm{T}=-4.8\vec{\jmath}\,\mu\mathrm{T}$

siendo el campo magnético en este punto

$\vec{B}_Q=\vec{B}_{Q1}+\vec{B}_{Q2}+\vec{B}_{Q3}=-8.0\vec{\jmath}\,\mu\mathrm{T}$

Tres hilos en paralelo y en serie

De Laplace

Contenido

1 Enunciado

2 Intensidades de corriente

2.1 Resistencias

2.2 Antes de abrir los interruptores

2.3 Con los interruptores abiertos

3 Potencia por efecto Joule

3.1 Antes de abrir los interruptores

3.2 Con los interruptores abiertos

4 Campo magnético

4.1 Antes de abrir los interruptores

4.1.1 Punto P

4.1.2 Punto Q

4.2 Con los interruptores abiertos

4.2.1 Punto P

4.2.2 Punto Q

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES