Test del segundo parcial 2017-2018 (Física II GIE)
De Laplace
Contenido |
1 Tres cargas en un triángulo
Tres cargas puntuales se encuentran en los vértices de un triángulo equilátero de lado b. Dos de ellas valen q1 y la tercera vale q2. ¿Cuánto debe valer q2 para que la energía electrostática del sistema sea nula?
- A − 2q1.
- B − q1 / 2.
- C − q1.
- D + 2q1.
- Solución
La respuesta correcta es la B.
2 Dos cargas y dipolo
Un dipolo puntual está situado en el campo eléctrico de dos cargas iguales, estando el dipolo y las cargas como indica la figura. El par debido a las cargas es tal que…
- A tiende a girar el dipolo en sentido positivo (antihorario).
- B tiende a girar el dipolo en sentido negativo (horario).
- C es nulo. El dipolo no tiende a girar.
- D puede ser tanto horario como antihorario, dependiendo del signo de las cargas.
- Solución
La respuesta correcta es la D.
3 Campo de un disco
Un disco de radio b está cargado uniformemente de forma que produce en su eje un campo de la forma 
. ¿Cuál de las siguientes figuras representa E(z)?
| 
|
| A | B |
|---|---|
| 
|
| C | D |
- Solución
La respuesta correcta es la B.
4 Esfera cargada en volumen
Una esfera de radio b se encuentra cargada con una densidad ρ(r) = Ar siendo 
la distancia al centro de la esfera y 
el vector de posición respecto al centro de la esfera.
4.1 Pregunta 1
¿Cuánto vale la carga total de la esfera?
- A πAb4.
- B Ab2 / 2.
- C 4πAb4 / 3.
- D 4πArb3 / 3.
- Solución
La respuesta correcta es la A.
4.2 Pregunta 2
Para esta esfera, ¿cuánto vale el campo eléctrico a una distancia r del centro, con r<b?
- A
.
- B
.
- C
.
- D
- A
- Solución
La respuesta correcta es la C.
5 Conductor con hueco
Un conductor esférico de radio c, contiene en su interior un hueco, también esférico, de radio b. En el interior de esta cavidad se halla una carga puntual q0. El conductor se halla conectado a una fuente de tensión V0. No hay más conductores ni cargas en el sistema. ¿Cuánto vale la carga total del conductor?
- A
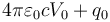
- B − q0
- C
- D
- A
- Solución
La respuesta correcta es la D.
6 Conductor con capa de dieléctrico
Un conductor esférico tiene radio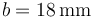 
. Esta esfera se forra con una capa de dieléctrico de permitividad relativa 
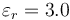, de radio interior b y exterior 
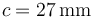. Si la esfera se encuentra a un potencial V0 ¿cómo es el circuito equivalente de este sistema?
- A Dos condensadores en serie de capacidades
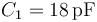y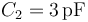 
.
- B Dos condensadores en serie de capacidades 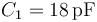y
.
- C Un condensador de capacidad .
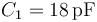- D Dos condensadores en paralelo de capacidades 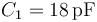y .
- A Dos condensadores en serie de capacidades
Datos: Capacidad de un condensador esférico: 
.
Constante dieléctrica del vacío 
- Solución
La respuesta correcta es la A.
7 Cuatro placas conductoras
Se tiene el sistema de cuatro placas conductoras de la figura, todas de la misma superficie y situada cada placa a la misma distancia de la siguiente. Entre las placas hay vacío. Inicialmente las dos placas centrales están aisladas y descargadas. De las placas exteriores una está a tierra y la otra a una tensión V0. Sin desconectar las placas exteriores, se cierra el interruptor que conecta las dos placas centrales. Una vez alcanzado de nuevo el equilibrio, ¿cuál es la energía electrostática del sistema comparada con la que había antes de cerrar el interruptor, Uef / Uei?
- A 100%.
- B 67%.
- C 150%.
- D 33%.
- Solución
La respuesta correcta es la C.
