Test del primer parcial 2016-2017 (GIE)
De Laplace
Contenido |
1 Velocidad variable
Un volumen de 1 μm³ ¿A cuántos cm³ equivale?
- A 10 − 12
- B 10 − 7
- C 10 − 4
- D 10 − 8
- Solución
La respuesta correcta es la A.
Una micra son 10 − 4 cm. Al elevarlo al cubo resultan 10 − 12 cm³
2 Movimiento armónico simple
Un movimiento armónico simple tiene por elongación
¿Cuánto vale su fase inicial o constante de fase?
- A + π / 2
- B + π / 4
- C 0
- D − π / 4
- Solución
La respuesta correcta es la D.
Cuando se escribe el movimiento armónico simple en las formas equivalentes
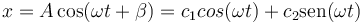
la constante de fase viene dada por
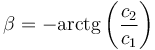
En nuestro caso
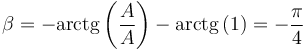
3 Movimiento plano
¿Cuál de las siguientes condiciones no define un movimiento plano?
- A El vector binormal es constante.
- B El vector de posición puede escribirse en la forma
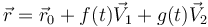, con 
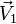y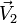 
constantes.
- C En todo instante se anula el producto mixto
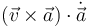
- D El radio de curvatura es constante.
- Solución
La respuesta correcta es la D.
Que el radio de curvatura constante no es suficiente para definir un movimiento plano es fácil de ver sin más que considerar el ejemplo de la hélice, que tiene un radio de curvatura constante, pero es un movimiento tridimensional.
4 Velocidad parabólica
La velocidad de una partícula como función del tiempo viene dada por la gráfica parabólica siguiente:
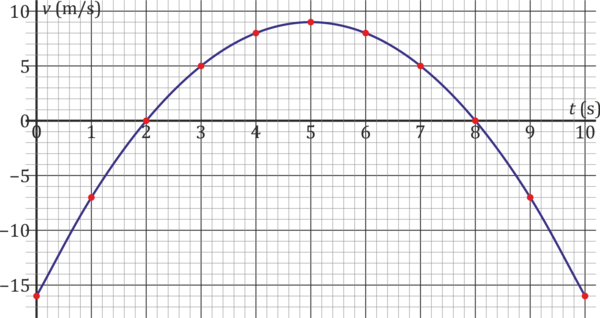
4.1 Pregunta 1
¿Cuánto mide el desplazamiento de la partícula entre t=0s y t=10s?
- A 0m
- B -3.33m
- C 6.66m
- D -6.66m
- Solución
La respuesta correcta es la C.
Hallamos primero la ecuación de la velocidad como función del tiempo. Por ser una parábola es de la forma
Como se anula en t = 2 y t = 8 (segundos, usamos unidades fundamentales del SI) y en t = 0 vale -16, queda
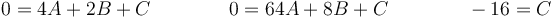
Restando
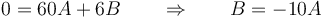
Sustituimos
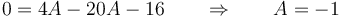
Por tanto la parábola es de la forma
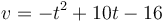
Integramos respecto al tiempo para hallar el desplazamiento
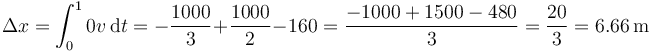
4.2 Pregunta 2
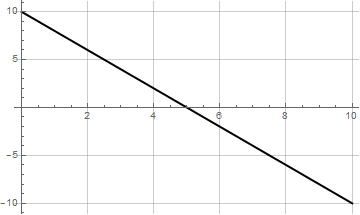
¿Cuál de las siguientes gráficas es la de la aceleración de la partícula?
| 
|
| A | B |
|---|---|
| 
|
| C | D |
- Solución
La respuesta correcta es la B.
La velocidad es una función cuadrática, por lo que la aceleración, su derivada, debe ser una recta. Además, la velocidad es creciente en la primera mitad del intervalo y decreciente en la segunda, por lo que la aceleración debe ser poitiva en la primera mitad y negativa en la segunda. Por ello, su gráfica es la B.
Evidentemente, también puede demostrarse derivando respecto al tiempo la expresión de la velocidad.
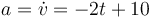
5 Momento de un vector
¿Qué dirección tiene el momento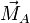 
de un vector 
respecto a un punto A?
- A Es ortogonal al plano definido por A y la recta soporte de .
- B Va en la dirección de la recta perpendicular a y que pasa por A
- C Es paralelo a
- D Va en la dirección de la recta que pasa por A y por el punto de aplicación de
- A Es ortogonal al plano definido por A y la recta soporte de
- Solución
La respuesta correcta es la A.
El momento de un vector aplicado en P es, por definición,
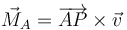
y este vector es ortogonal a los dos vectores que se multiplican y por tanto al plano que definen.
6 Movimiento en cilíndricas
Si las coordenadas cilíndricas de una partícula varían como
¿Cuál de las gráficas siguientes puede representar la trayectoria de la partícula?
| 
|
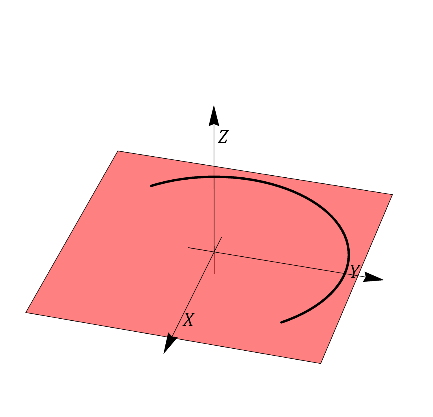
| A | B |
|---|---|
| 
|
| C | D |
- Solución
La respuesta correcta es la B.
Al ser θ = π / 4 constante, la trayectoria debe estar en un plano vertical que forma este ángulo con el eje OX. Esto nos deja con las opciones B y D, pero en este movimiento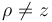 
. Por tanto no puede ser la opción D y solo queda la B.
Concretamente, el movimiento se realiza sobre un meridiano de una esfera de radio A.
