Test del Examen Parcial 2015-2016 (1ª parte) (GIE)

De Laplace

Contenido

1 Gráfica de un ciclo Otto
2 Condensador con dieléctrico
3 Enunciado de Kelvin-Planck
4 Fuerza magnética entre cargas puntuales
5 Posibilidad de un proceso
6 Corrientes de Foucault

1 Gráfica de un ciclo Otto

¿Cuál de las siguientes figuras corresponde a un ciclo Otto ideal en un diagrama pV?

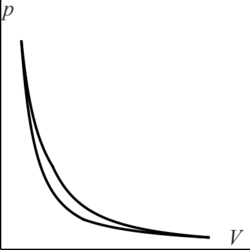
A	B


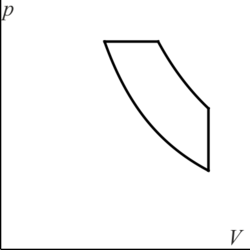
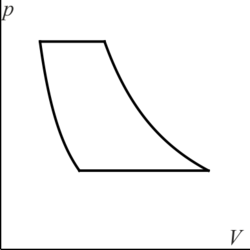
C	D

Solución

La respuesta correcta es la A.

El ciclo Otto ideal está formado por dos adiabáticas y dos isócoras. Estas dos últimas, que son procesos a volumen constante, se representan como líneas verticales en un diagrama pV.

2 Condensador con dieléctrico

Se tiene un condensador de placas planas y paralelas entre las cuales hay vacío y entre las que se establece una diferencia de potencial $V 0$ . Sin desconectar las placas de la fuente se rellena el espacio entre las placas con un dieléctrico de permitividad relativa $\varepsilon_r = 2.0$ . Como resultado, la energía almacenada en el condensador\ldots

A se reduce a la mitad.
B no cambia.
C aumenta al doble.
D aumenta al cuádruple.

Solución

La respuesta correcta es la C.

Para un voltaje dado, la energía almacenada en un condensador es

$U_\mathrm{e}=\frac{1}{2}CV_0^2$

siendo la capacidad

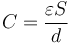
$C=\frac{\varepsilon S}{d}$

En este caso, en el que la permitividad del dieléctrico es el doble de la del vacío

$\varepsilon = 2.0\varepsilon_0\qquad \Rightarrow\qquad C=2C_0$

y para la energía

$U_\mathrm{e}=\frac{1}{2}(2C_0)V_0^2 =2\left(\frac{1}{2}C_0V_0^2\right)=2U_0$

3 Enunciado de Kelvin-Planck

¿Cuál de los siguientes es el enunciado de Kelvin-Planck del segundo principio de la termodinámica?

A No es posible un proceso cuyo único resultado sea el paso de calor desde un foco frío a uno caliente.
B En todo proceso adiabático real, la variación de la entropía del sistema es siempre positiva o nula.
C No es posible una máquina térmica cuyo rendimiento sea superior al de una máquina térmica reversible que opere entre las temperaturas extremas del ciclo.
D No es posible una máquina térmica que tome calor de un solo foco térmico y lo transforme íntegramente en trabajo.

Solución

La respuesta correcta es la D.

4 Fuerza magnética entre cargas puntuales

Dos cargas positivas se mueven con la misma rapidez, pero en direcciones diferentes. Indique cuál de las siguientes figuras indica adecuadamente la dirección y sentido de la fuerza magnética que cada una ejerce sobre la otra (⊙: hacia afuera del papel; ⊗: hacia adentro).

A	B


C	D

Solución

La respuesta correcta es la B.

5 Posibilidad de un proceso

Una cierta cantidad de aire seco ( $γ = 1.4$ ) se encuentra dentro de un recipiente adiabático con pistón también adiabático, ocupando un volumen $V A$ a una presión $p A$ y a una temperatura $T A$ . Se supone que se realiza una expansión en la que el volumen pasa a ser $2 V A$ y la temperatura baja a $(3 / 4) T A$ . Este proceso es…

A Posible e irreversible.
B Posible y reversible.
C Imposible.
D No hay información suficiente para responder a esta pregunta.

Solución

La respuesta correcta es la C.

6 Corrientes de Foucault

Las corrientes de Foucault son las inducidas en el interior de un material óhmico. Supóngase que se tiene un cilindro de radio $b$ y altura $h$ de un material de conductividad $σ$ sometido a un campo magnético variable, en la dirección del eje del cilindro $\vec{B}=B(t)\vec{k}$ . Para modelar las corrientes de Foucault podemos suponer el cilindro compuesto de espiras de radio $r$ , anchura $d r$ y altura $d z$ . ( $\dot{B}=\mathrm{d}B/\mathrm{d}t$ )